В измерениях МСМ мы собираем информацию о распределении поля рассеяния над образцом, обычно в одном слое на заданной высоте над образцом в ходе одного измерения. Вместе с этим сигналом мы также собираем информацию о топографии так же, как и в других техниках СЗМ.
Функции для работы с данными МСМ можно найти в меню → → . Отдельные модули и алгоритмы обработки данных, описываемые в следующих абзацах, можно разбить на следующие категории:
- вспомогательные функции, такие как преобразование различных величин в градиент силы.
- модули для моделирования отклика МСМ на различные образцы (например, среду для перпендикулярной записи или тонкою полоску плёнки с электрическим током),
- модули основанного на использовании известных образцов анализа зонда и
- набор функций для работы с многоканальными данными, например, данными, измеренными с разнонаправленной намагниченностью зонда.
Последняя категория включает в себя функции общего назначения, такие как арифметика над данными, которые могут складывать и вычитать изображения и комбинировать их другими способами используя арифметические выражения, или взаимно кадрировать, которая обрезает изображения до их области пересечения (что обычно требуется до выполнения других операций с множественными данными).
Сложение и вычитание измерений проведённых с двумя разными направлениями намагниченности зонда было предложено как способ потенциально улучшить разделение вкладов от магнитного взаимодействия и других видов взаимодействий [Cambel11]. Если также доступны измерения с различными направлениями протекания тока, то у нас будет четыре возможных варианта того, как будут взаимно ориентированны электростатические и магнитные силы. Все четыре могут комбинироваться с использованием арифметики над данными чтобы подавить шум в данных.
Функция производит преобразование различных измеренных величин в градиент силы. Входное изображение должно соответствовать одной из величин, для которых данное преобразование реализовано: фазе, сдвигу частоты или амплитуде (в Вольтах или метрах). Тип входных данных определяется автоматически и показывается как выбор входной величины в верхней части окна.
Преобразование требует ввести параметры инструмента и измерения, которые различаются в зависимости от типа входных данных и могут включать в себя константу упругости, добротность или начальную амплитуду.
Несколько модулей, различающихся по используемым алгоритмам, моделируют распределение поля рассеяния в плоскости над поверхностью образца. Ни один из них не работает с общим случаем магнитной среды, например, решая уравнения Пуассона для того чтобы найти распределение магнитного поля из объёмной намагниченности образца, поскольку на данный момент этот подход кажется излишне требовательным к вычислительным ресурсам для пакета общего назначения, которым является Gwyddion (по крайней мере на данное время). Модули настроены чтобы моделировать несколько типичных случаев, описанных в литературе, где существует достаточное количество допущений о намагниченности образца, что делает расчёт поля рассеяния доступным с помощью простых методов.
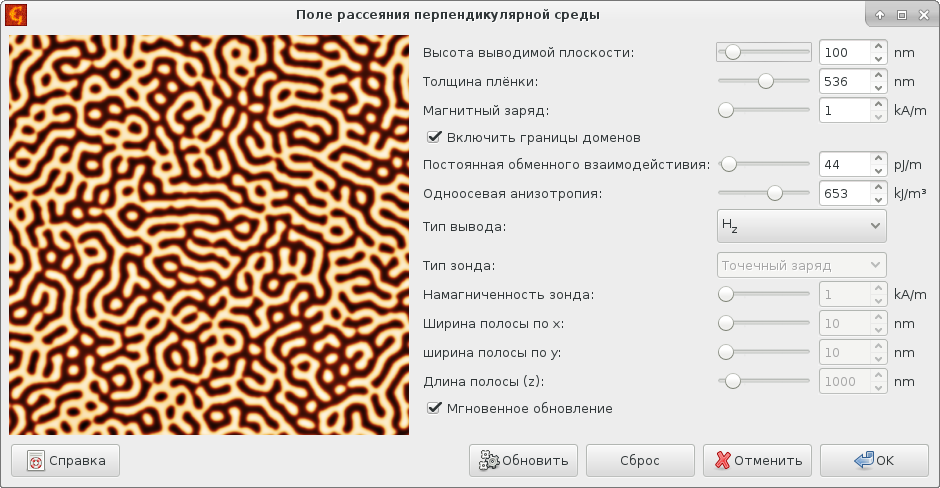
Модуль для работы с перпендикулярной средой основан на работах Х. Хуга (H. Hug) [Hug98] и С. Вока (S. Vock) [Vock11][Vock14]. Распределение поля рассчитывается на основе известного распределения намагниченности в слое, в направлении z намагниченность считается постоянной для каждой точки слоя и меняется исключительно если мы движемся в плоскости слоёв. Изначально намагниченность описывается как двоичное изображение (намагниченность вверх/вниз, заданная маской), к ней можно добавить стенки доменов заданной толщины. Затем расчёты проводятся в Фурье-пространстве. Помимо распределения магнитного поля также могут быть рассчитаны результаты использования простых функций зонда, известных аналитически (точечный заряд, прямоугольный параллелепипед), и численно посчитанные производные получаемых в результате сил.
Предполагая распределение поверхностного заряда +σ(x, y) на верхней поверхности среды и противоположный заряд −σ(x, y) на нижней поверхности мы можем использовать анализ Фурье для получения распределения поля. Сначала мы преобразуем поверхностные заряды в Фурье-пространство:
Опционально мы можем даже предположить, что между доменами существуют блоховские стены некоторой толщины δw, делая свёртку σ(x, y) перед расчётом с оператором размытия
, где толщина стенки может быть выражена через постоянную обменной жесткости A и постоянную одноосевой анизотропии Ku как
Затем можно рассчитать Фурье-компоненты поля рассеяния на высоте z, создаваемого верхней и нижней поверхностями плёнки толщиной d как
Применив обратное преобразование Фурье можно получить магнитное поле рассеяния над образцом:
оставаясь в Фурье-пространстве можно рассчитать силу, действующую на простой зонд в форме бруска сечением bx × by, длиной L и намагниченностью Mt, умножая длину компонент поля рассеяния AHzz, d на аналитическую функцию передачи силы:
Поскольку Gwyddion способен не только работать с измеренными данными, но и синтезировать множество различных искусственных поверхностей, существует множество подходов к работе с модулем моделирования перпендикулярной среды, создавая различные поля от более или менее реалистичных образцов. Следующий рисунок демонстрирует несколько примеров таких модельных масок и получаемых в результате данных.

Результат работы модулей синтеза поверхностей, использованных для моделирования данных МСМ перпендикулярной среды: плёнка в виде колонн, фрактальная шероховатость, домены в модели Изинга, решетка, бублики.
Для параллельной среды диапазон возможных расчётов гораздо меньше — основываясь на аналитической модели можно рассчитать поле над полосами, ориентированными в левом и правом направлении (подобно жесткому диску). Это основывается на работе [Rugar90], дающей следующий набор уравнений для отдельных преобразований
где Mr это остаточная намагниченность магнитного слоя, z расстояние от зонда до слоя, a ширина переходного слоя и d толщина слоя.
Полосы не обязательно должны быть одинакового размера. В результате могут быть построены интенсивности полей в направлении осей x и z и рассчитана сила в направлении z, основанная на известных передаточных функциях зонда (таких же, как и для перпендикулярной среды). Также могут быть (численно) рассчитаны её производные.
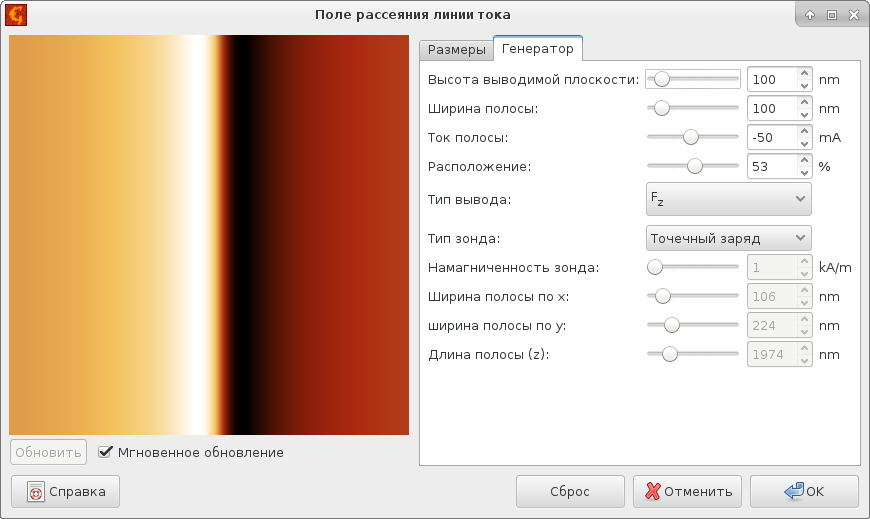
Подобным же образом аналитические выражения можно использовать для моделирования поля над тонким проводником с текущим по нему током. Для этого можно использовать модуль поле линии тока, основанный на уравнении из [Saida03]:
для полосы шириной w по которой течёт ток I.
Поскольку все модули моделирования могут также использоваться для добавления результата к имеющимся данным, вызывая модуль несколько раз мы можем также моделировать плоскую катушку (или, точнее, две линии с противоположным направлением тока). Это показано на следующих рисунках.
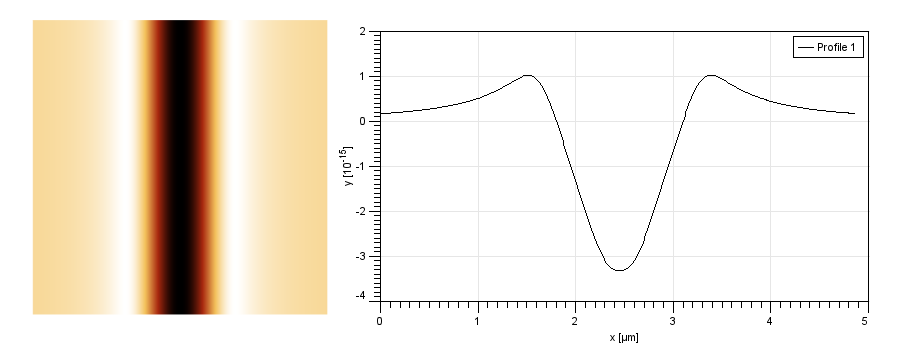
Распределение поля рассеяния над двумя параллельными линиями тока с противоположными направлениями его протекания.
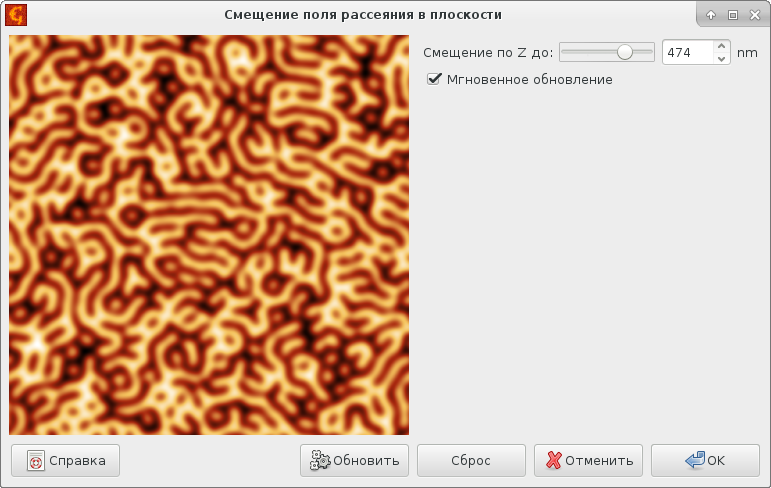
Алгоритмы для расчёта поля рассеяния с помощью преобразования Фурье могут также использоваться чтобы сдвигать поле с одной высоты слоя на другую. Это работает если мы удаляемся от образца (размывая данные), но это не даёт хороших результатов если мы приближаемся к образцу (расчёт расходится). Основываясь на [Hug98] процедура должна быть следующей:
- Поле Hz(r) пересчитывается преобразованием Фурье в его спектральную интерпретацию AHz(k),
- Спектральные компоненты умножаются на масштабирующий множитель exp(kd) где d расстояние между двумя плоскостями (положительное или отрицательное),
- Обратное преобразование Фурье используется чтобы получить значения поля в нормальном пространстве.
Можно поиграть с этим алгоритмом в модуле сдвига поля как показано на следующем рисунке.
Подобный подход может использоваться для обратной операции — оценки разницы высоты сканирования между двумя наборами данных. Здесь используется простая техника поиска прямым перебором чтобы найти сдвиг в направлении z, который будет давать наилучшее соответствие двух окликов МСМ. Интерфейс пользователя показан на рис. 8. Потенциальным применением данного модуля может быть поиск реальной высоты подъёма вместо указанной, хотя здесь могут проявляться проблемы на реальных данных при наличии каких-то паразитных взаимодействий.
Несколько подходов по решению проблем с разрешением зондов МСМ было предложено. Можно анализировать профили поперёк перпендикулярного образца или использовать спектр мощности для оценки разрешения зонда, т.е. пытаясь найти, где спектр мощности исчезает до уровня шума. См. Оценку передаточной функции для описания метода оценки передаточной функции, реализованного в настоящее время в Gwyddion. Эта техника в действительности не является специфичной для МСМ и может быть использована универсально для оценки передаточной функции ПФ (или функции рассеяния точки PSF) в любом режиме СЗМ, если можно записать или смоделировать пример идеального отклика. Математические и алгоритмические детали о том, как данные магнитных измерений обрабатываются в модулях работы с передаточной функцией можно найти в статье Nečas19.
Чтобы проиллюстрировать всю процедуру получения количественных результатов измерения МСМ мы приводим ниже пример оценки передаточной функции на известном образце и и обработку данных, полученных с неизвестного образца, основанную на этой передаточной функции.
Началом процесса будет использование данных, измеренных на известном образце. Здесь использовался многослойный образец, изготовленный IFW Dresden, для которого поле рассеяния над образцом может быть рассчитано на основе известного распределения доменов и известных свойств образца. Вместе с ними доступны тестовые данные «неизвестного» образца, предоставленного National Physical Laboratory, которые доступны для скачивания в одном входном файле.
Чтобы пройти процедуру шаг за шагом и получить такие же результаты, как представлены в файле с обработанными данными, необходимо пройти следующую последовательность шагов:
[Hug98] H. J. Hug, B. Stiefel, P. J. A. van Schendel, A. Moser, R. Hofer, S. Martin, H.-J. Gutherodt, S. Porthun, L. Abelmann, J. C. Lodder, G. Bochi and R. C. O’Handley: J. Appl. Phys. (1999) Vol. 83, No. 11
[Vock11] S. Vock, Z Sasvari, C. Bran, F. Rhein, U. Wolff, N. S. Kiselev, A. N. Bogdanov, L. Schiltz, O. Hellwig and V. Neu: IEEE Trans. on Magnetics, 47 (2011) 2352
[Vock14] S. Vock, C. hengst, M. Wolf, K. Tschulik, M. Uhlemann, Z. Sasvari, D. Makarov, O. G. Schmidt, L Schultz and V. Neu: Appl. Phys. Lett 105 (2014) 172409
[Rugar90] D. Rugar, H. J. Mamin, P. Guethner, S. E. Lambert, J. E. Stern et al.: J. Appl. Phys. 68 (1990) 1169
[Saida03] D. Saida, T. Takahashi: Jpn. J. Appl. Phys. 42 (2003) Pt. 1, No. 7B
[Cambel11] V. Cambel, D. Gregusova, P. Elias, J. Fedor, I. Kostic, J. Manka, P. Ballo: Journal of Electrical Engineering, 62 (2011) 37–43
[Necas19] D. Nečas, P. Klapetek, V. Neu, M. Havlíček, R. Puttock, O. Kazakova, X. Hu, L. Zajíčková, Scientific Report, 9 (2019) 3880