La transformée de Fourier bi-dimensionnelle peut être utilisée à partir de → → dans lequel est implémentée une transformée de Fourier rapide (FFT, Fast Fourier Transform). La transformée de Fourier décompose un signal selon ses composantes harmoniques, elle est ainsi très utile pour l'analyse des fréquences spatiales présentes dans les données SPM.
Le module FFT 2D propose plusieurs types de sortie :
- Module – valeur absolue des coefficients de Fourier complexes, propoportionnelle à la racine carrée de la densité spectrale de puissance (PSD, Power Spectral Density).
- Phase – phase des coefficients complexes (rarement utilisé).
- Partie réelle – partie réelle des coefficients complexes.
- Partie imaginaire – partie imaginaire des coefficients complexes.
ainsi que certaines combinaisons pour des raisons pratiques.
Des sections radiales de la PSD bi-dimensionnelle peuvent être aisément obtenus avec → → . Plusieurs autres fonctions générant des densités spectrales sont décrites dans la section Analyse Statistique. Il est aussi possible de filtrer des images dans le domaine fréquentiel en utilisant les filtres de FFT uni-dimensionnels et bi-dimensionnels, ou simplement la séparation fréquentielle.
Pour comparer des textures indépendemment de l'échelle et de la rotation, il est utile de transformer les coordonnées fréquentielles cartésiennes de la PSDF en coordonnées définies par le logarithme de la fréquence spatiale et de sa direction. L'échelle et la rotation deviennent alors de simples translations selon les nouvelles coordonnées. La fonction → → calcule directement la PSDF transformée. La coordonnée horizontale sans dimension est l'angle (de 0 à 2π), et la coordonnée verticale est le logarithme de la fréquence spatiale. iL est possible d'adoucir la PSDF à l'aide d'un filtre gaussien de largeur donnée avant de faire la tranformation.
Notez que la transformée de Fourier traite les données comme si elles s'étendaient à l'infini, ce qui implique des conditions aux limites périodiques. Comme les données réelles ne possèdent pas ces propriétés, il est nécessaire d'utiliser des fonctions de fenêtrage pour supprimer les données sur les bords de l'image. Si vous n'en choisissez aucune, la FFT traitera les données avec une fonction de fenêtrage rectangulaire qui donne une mauvaise image de la transformée, donnant ainsi un spectre de Fourier erroné.
Gwyddion propose plusieurs fonctions de fenêtrage. La plupart d'entre elles sont basées sur des fonctions sinus ou cosinus qui atténuent correctement les données sur les bords de l'image. Dans la table des formules de fenêtrage qui suit, la variable indépendante x appartient à l'intervalle [0, 1] qui correspond à l'abscisse normalisée ; pour simplifier la notation la variable ξ = 2πx est utilisée dans certaines formules. Les types de fenêtrage disponibles sont données dans la table qui suit :
| Nom | Formule |
|---|---|
| Aucun | 1 |
| Rectangle | 0.5 aux bords, 1 partout ailleurs |
| Hann | |
| Hamming | |
| Blackmann | |
| Lanczos | |
| Welch | |
| Nutall | |
| Plateau | |
| Kaiserα | , où I0 est la fonction de Bessel modifiée d'orde zéro et α est un paramètre |
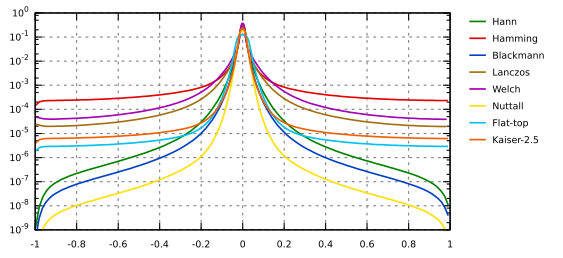
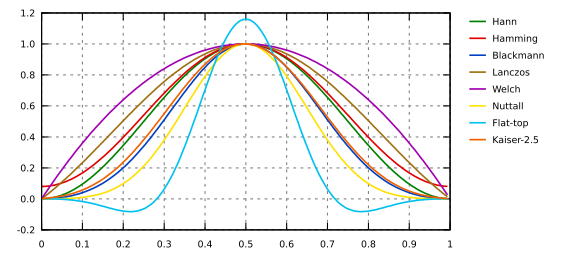
Enveloppes des réponses fréquentielles de fonctions de fenêtrage : Hann, Hamming, Blackmann, Lanczos, Welch, Nutall, plateau, Kaiser 2,5.
→ →
Le filtrage de Fourier est un excellent moyen de supprimer le bruit d'une image en se basant sur l'analyse fréquentielle. La transformée de Fourier de l'image est d'abord calculée, puis un filtre est appliquée à cette transformée. La transformée inverse est finalement appliquée pour obtenir l'image filtrée. Gwyddion utilise la transformée de Fourier rapide (FFT) pour rendre ce calcul beaucoup plus rapide.
Pour le filtre FFD 1D, les fréquences à supprimer du spectre (type de suppression : annuler) ou réduites aux valeurs des fréquences avoisinantes (type de suppression : supprimer) peuvent être sélectionnées en marquant les zone souhaitées dans le graphe du spectre. La sélection peut être facilement inversée en utilisant le type de filtre (marqué ou non marqué). Le filtrage FFT 1D peut être utilisé pour la direction verticale ou horizontale.
→ →
Le filtrage FFT 2D agit de manière similaire à la version 1D (voir plus haut), mais en utilisant une transformée de Fourier 2D. Les fréquences à filtrer doivent donc être sélectionnées à l'aide d'un éditeur de masque en 2D. Comme les fréquences sont liées au centre de l'éditeur (qui correspond à la fréquence nulle), le masque peut être automatiquement lié au centre (origine des coordonnées spectrales) lors de son édition. Plusieurs types d'affichage et de sortie sont disponibles, dont la description est explicite – l'image ou les coefficients de la FFT (ou bien les deux) peuvent être extraits par le module.
→ →
Une alternative simple au filtrage FFT 2D consiste à séparer les fréquences spatiales hautes et basses en utilisant un filtre passe-haut ou passe-bas. Le module de séparation fréquentielle peut générer l'image basse ou haute fréquence, ou bien les deux à la fois, en fonction du Type de sortie sélectionné.
La Coupure permet de définir la fréquence de coupure, affichée en fraction de la fréquence de Nyquist, ainsi que la période spatiale correspondante. Si Largeur des bords (elle aussi donnée en fraction de la fréquence de Nyquist) est nulle, le filtre aura des bords droits. Pour une valeur non-nulle, la transition aura la forme de la fonction d'erreur (erf), avec la largeur spécifiée.
Le filtrage fréquentiel peut générer des artefatcts sur les bords des l'image. Plusieurs manières de gérer les bords sont donc proposées, en complément de Aucun qui n'est réellement utile que pour les données périodiques (ou bien si la continuité est assurée entre les bords). Les options Laplace et Miroir étendent respectivement l'image à l'aide de l'équation de Laplace ou par mise en miroir de l'image, exactement de la même manière que la fonction Étendre. L'option Connexion douce applique aux lignes et aux colonnes la méthode d'extension uni-dimensionnelle utilisée dans l'outil Rugosité pour supprimer les artefacts aux bords.