La transformée en ondelettes est similaire à la transformée de Fourier (et encore plus à la transformée de Fourier locale) avec une fonction de mérite complètement différente. La différence principale est la suivante : la transformée de Fourier décompose le signal en sinus et en cosinus, c'est-à-dire en fonctions localisées dans l'espace de Fourier ; contrairement à la transformée en ondelettes qui utilise des fonctions localisées à la fois dans l'espace réel et dans l'espace de Fourier. De manière générale, la transforméee en ondelettes peut être exprimée avec l'équation suivante :
où le symbole * désigne le conjugué complexe et ψ est une fonction donnée. Cette fonction peut être choisie arbitrairement à condition qu'elle obéisse à certaines règles.
Comme on peut le voir, la transformée en ondelettes est en fait un ensemble infini de diverses transformées, dépendant de la fonction de mérite utilisée pour la calculer. C'est la raison pour laquelle nous pouvons entendre parler de la « transformée en ondelettes » dans des contextes et applications très divers. Il existe aussi de nombreuses manières de classer les types de transformées en ondelettes. Nous ne présentons ici que la division basée sur l'orthogonalité des ondelettes. Nous pouvons utiliser les ondelettes orthogonales pour le développement en ondelettes discret et les ondelettes non-orthogonales pour le développement en ondelettes continu. Ces deux transformées possèdent les propriétés suivantes :
- La transformée en ondelettes discrète retourne un vecteur de données de même longueur que les données d'entrée. Généralement la plupart des valeurs de ce vecteur sont pratiquement nulles. Cela vient du fait qu'elle décompose en un ensemble d'ondelettes (fonctions) orthogonales par translation et par homothétie. On décompose ainsi le signal en un nombre égal ou inférieur de coefficients du spectre d'ondelettes que le nombre de points de données du signal. Un tel spectre d'ondelettes est très bon pour le traitement du signal et la compression, par exemple, car nous n'obtenons ici aucune information redondante.
- La transformée en ondelettes continue retourne quant à elle un vecteur de dimension supérieure de un à celle des données d'entrée. Pour des données 1D nous obtenons une image du plan temps-fréquence. On peut ainsi aisément visualiser l'évolution fréquentielle pendant la durée du signal et comparer son spectre avec ceux d'autres signaux. Comme on utilise ici un ensemble d'ondelettes non-orthogonales, les données sont hautement corrélées, on a donc dans ce cas une redondance élevée. Ceci permet de voir le résultat sous une forme plus « humaine ».
Pour plus de détails sur la trasnformée en ondelettes vous pouvez jeter un coup d'œil sur les nombreuses ressources disponibles sur internet, ou par exemple sur [1].
Ces deux transformées sont implémentées dans la librairie de traitement des données de Gwyddion, et les modules utilisant la transformée en ondelettes sont accessibles dans le menu → menu.
La transformée en ondelettes discrète (DWT, Discrete Wavelet Transform) est une implémentation utilisant un ensemble discret d'échelles et de translations d'ondelettes obéissant à certaines règles. En d'autres termes, cette transformée décompose le signal en un ensemble d'ondelettes mutuellement orthogonales, ce qui constitue la différence principale avec la transformée en ondelettes continue, ou son implémentation en séries discrètes dans le temps parfois appelée transformée en ondelettes continue discrète dans le temps (DT-CWT, discrete-time continuous wavelet transform).
L'ondelette peut être construite à partir d'une fonction d'échelle décrivant les propriétés d'échelle du signal. La restriction d'orthogonalité avec les translations discrètes implique certaines conditions mathématiques, par exemple l'équation de dilatation
où S est un facteur d'échelle (prenant généralement une valeur de 2). De plus, la zone entre les fonctions doit être normalisée et la fonction d'échelle doit être orthogonale par translation, c'est-à-dire qu'on a
Après introduction de conditions supplémentaires (les réstrictions précédentes ne produisent pas une solution unique) nous pouvons obtenir le résultat de toutes ces équations, c'est-à-dire un ensemble fini de coefficients ak définissant la fonction d'échelle ainsi que l'ondelette. L'ondelette est obtenue à partir de la fonction d'échelle grâce à N où N est un entier pair. L'ensemble des ondelettes forme alors une base orthogonale que nous utilisons pour décomposer le signal. Notez qu'en général seuls quelques coefficients ak sont non nuls, ce qui simplifie les calcul.
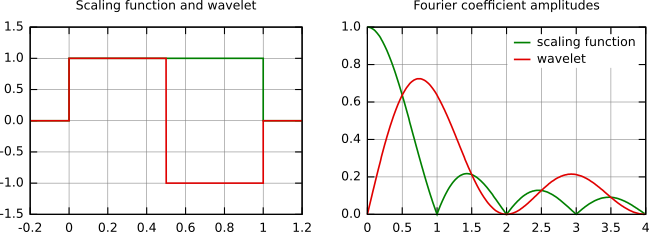
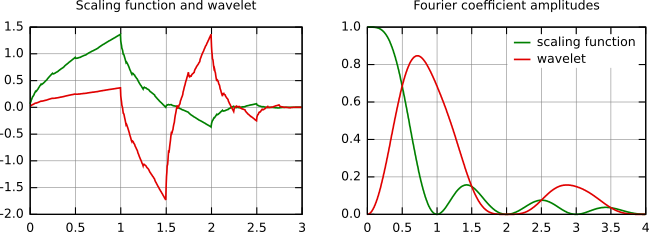
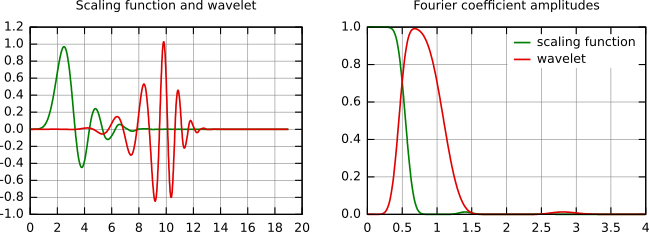
Quelques fonctions d'échelle et d'ondelettes sont présentées dans la figure qui suit. La famille Daubechies est la famille la plus connue des ondelettes orthonormales. Ses ondelettes sont généralement dénommées par le nombre de coefficients ak non nuls, on parlera donc d'ondelettes Daubechies 4, Daubechies 6, etc. Pour faire simple, les fonctions deviennent plus douces avec un nombre croissant de coefficients d'ondelettes. Comparez par exemple les ondelettes Daubechies 4 et 20 ci-dessous. La fonction la plus simple, l'ondelette de Haar, utilise une fonction porte commme fonction d'échelle.
Il existe plusieurs types d'implémentation de l'algorithme DWT. Le plus connue et aussi le plus ancien est l'algorithme (pyramidal) de Malaat. Dans celui-ci deux filtres – un lissant et un non-lissant – sont construits à partir des coefficients d'ondelette, puis utilisés de manière récurrente pour obtenir les données pour toutes les échelles. Si le nombre total de données D = 2N est utilisé et que la longueur du signal est L, les premières D/2 donnée d'échelle L/2N - 1 sont calculées, puis les (D/2)/2 données d'échelle L/2N - 2, … pour obtenir finalement 2 données d'échelle L/2. Le résultat de cet algorithme est un ensemble de même longueur que celle des données d'entrée, dans lequel les données sont généralement classées de la plus grande à la plus petite échelle.
L'algorithme pyramidal est utilisé dans Gwyddion pour calculer la transformée en ondelettes discrète. La version 2D est accessible en utilisant le moduel DWT.
La transformée en ondelettes discrète peut être utilisée pour débruiter facileement et rapidement un signal. Si nous ne prenons qu'un nombre limité des coefficients les plus élevés dans le spectre de la transformée, et que nous appliquons la transformée inverses (en utilisant la même base d'ondelettes) nous pouvons obtenir un signal plus ou moins débruité. Il existe plusieurs façons de choisir les coefficients qui seront conservés. Le seuillaeg universel, le seuillage adaptatif d'échelle [2] et le seuillage adaptatif d'échelle et d'espace [3] sont implémentées dans Gwyddion. La détermination du seuil pour ces différentes méthodes se fait d'abord en évaluant la variance du bruit donnée par
où Yij correspond à tous les coefficients de la sous-bande de plus haute échelle de la décomposition (dans laquelle la majorité du bruit est supposée se trouver). La variance du bruit peut aussi être obtenue de manière indépendante, par exemple à partir de la variance du signal AFM lorsque celui-ci n'effectue pas de scan. Pour la sous-bande de plus haute fréquence (seuillage universel) ou pour chaque sous-bande (seuillage adaptatif d'échelle) ou pour le voisinnage de chaque pixel dans la sous-bande (seuillage adaptatif d'échelle et d'espace) la variance est calculée par la formule suivante
La valeur de seuil est finalement obtenue par
où
Lorsque le seuil est connu pour une échelle donnée, nous pouvons soit supprimer tous les coefficients inférieurs au seuil (seuillage dur), soit diminuer la valeur absolue de ces coefficients par la valeur du seuil (seuillage doux).
Le débruitage par transformée en ondelettes discrète est accessible par le menu → → .
La transformée en ondelettes continue (CWT, Continuous Wavelet Transform) est une implémentation de la transformée en ondelettes utilisant des échelles arbitraires ainsi que des ondelettes pratiquement arbitraires. Les ondelettes utilisées ne sont pas orthogonales et les données obtenues par cette transformée sont hautement corrélées. Nous pouvons aussi utiliser cette transformée pour les séries discrètes dans le temps, avec la limitation que les translations des plus petites ondelettes soient égales au pas d'échantillonnage des données. Cette transformée est parfois appelée transformée en ondelettes continue discrète dans le temps (DT-CWT, Discrete-Time Continuous Wavelet Transform), et il s'agit de la façon la plus répandue de calculée la CWT pour des applications réelles.
En principe la transformée en ondelettes continue fonctionne en utilisant directement la définition de la transformée en ondelettes, c'est-à-dire en calculant la convolution du signal par l'ondelette mise à l'échelle. Nous obtenons de cette manière pour chaque échelle un ensemble de longueur N identique à celle du signal. En utilisant M échelles choisies arbitrairement nous obtenons une matrice N×M représentant directement le plan temps-fréquence. L'algorithme utilisé pour ce calcul peut être basé sur une convolution directe ou par une convolution réalisée par une multiplication dans l'espace de Fourier (aussi appelée transformée en ondelettes rapide).
Le choix de l'ondelette utilisée pour la décomposition temps-fréquence est le point le plus important. Celui-ci a une influence sur la résolution en temps et en fréquence du résultat. Nous ne pouvons modifier de cette manière les caractéristiques de la transformée en ondelettes (les basses fréquences ont une bonne résolution fréquentielle mais une mauvaise résolution temporelle ; les hautes fréquences ont une bonne résolution temporelle et une mauvaise résolution fréquentielle), mais nous pouvons toutefois augmenter la résolution fréquentielle totale ou la résolution temporelle totale. Ceci est directement proportionnel à la largeur de l'ondelette utilisée dans l'espace réel et dans l'espace de Fourier. Si nous utilisons par exemple l'ondelette de Morlet (partie réelle – fonction cosinus amortie) nous pouvons espérer une haute résolution fréquentielle car cette ondelette est très localisée du point de vue des fréquences. A l'inverse, l'utilisation d'une ondelette de type dérivée gaussienne (DOG, Derivative of Gaussian) donnera une bonne résolution temporelle, mais une mauvaise résolution fréquentielle.
La transformée en ondelettes continue (CWT) est implémentée dans le module CWT accessible par le menu → → .