L'analyse de surfaces rugueuses nécessite généralement une approche statistique afin de déterminer certains caractéristiques représentatives. Gwyddion propose différentes manières d'effectuer cette analyse. Cette section présente les différents outils et modules statistiques présents dans Gwyddion, et donne aussi les équations de base utilisées pour développer les algorithmes mis en œuvre.
Les données de microscopie à balayage sont généralement représentées par des champs de données à deux dimensions de taille N×M, où N et M sont respectvement les nombres de lignes et de colonnes du champ de données. La surface réelle est notée Lx×Ly où Lx et Ly sont les dimensions le long des axes respectifs. L'échantillonnage (distance entre deux points adjacents du balayage) est noté Δ. On suppose que l'échantillonnage est identique selon les directions x et y, et que la hauteur de la surface à point (x, y) donné peut être décrit par une fonction aléatoire ξ(x, y) ayant certaines propriétés statistiques.
Notez que les données AFM sont généralement acquises selon des lignes le long de l'axe x, et que celles-ci sont ensuite concaténées pour former l'image en deux dimensions. La vitesse de balayage selon la direction x est par conséquent bien plus élevée que selon la direction y. Il en résulte que les propriétés statistiques des données AFM sont généralement calculées pour des profils selon x car ceux-ci sont moins affectés par le bruit de basse fréquence et les variations thermiques de l'échantillon.
On trouve parmi les quantités statistiques les propriétés basiques des hauteurs telles que la variance, l'asymétrie et le kurtosis. Les quantités accessibles dans Gwyddion à l'aide de l'outil statistiques sont les suivantes :
- Valeurs moyenne, minimale, maximale et médiane.
- Valeur RMS des irrégularités de la surface : cette quantité est calculée à partir de la variance des données.
- Valeur RMS des grains, qui ne diffère du RMS habituel que dans le cas où un masque est utilisé. La valeur moyenne est alors déterminée pour chaque grain (parties contiguës du masque ou de l'inverse du masque, en fonction du type de masque) et la variance est calculée à partie des valeurs moyennes des grains.
- Valeur Ra des irrégularités de hauteur : cette valeur est similaire à la valeur RMS, elle ne diffère que dans l'exposant (puissance) dans la somme de la variance des données. Dans le cas du RMS l'exposant est q = 2, la valeur Ra est calculée avec l'exposant q = 1 et la valeur absolue des données (moyenne nulle).
- Asymétrie de la distribution des hauteurs : calculée à partir du moment d'ordre 3 des données.
- Kurtosis de la distribution des hauteurs : calculée à partir du moment d'ordre 4 des données.
- Surface et surface projetée : calculées par simple triangulation.
- Inclinaison moyenne des facettes : calculée en moyennant les vecteurs normaux des facettes.
- Variation : calculée par l'intégrale des valeurs absolues du gradient local.
- Entropie différentielle estimée de la distribution des valeurs, calculée à partir de l'histogramme, tel que décrit dans la partie fonction d'entropie. Elle est affichée en unité naturelle d'information (nat).
Astuce
L'outil statistiques affiche par défaut les données en se basant sur l'image entière. Si vous ne souhaitez analyser qu'une partie de l'image il suffit de sélectionner celle-ci dans la fenêtre des données. La fenêtre de l'outil mettra automatiquement à jour les nouvelles données basées sur la zone sélectionnée. Si vous souhaitez obtenir les statistiques de l'image entière, il suffit de cliquer une seule fois sur l'image, et l'outil se réinitialisera.Les valeurs de RMS (σ), asymétrie (γ1), et kurtosis (γ2) sont calculées à partir des moments de i-ième ordre μi selon les formules suivantes :
L'aire d'une surface est évaluée selon la méthode suivante. Soient zi pour i = 1, 2, 3, 4 les valeurs pour quatre points voisins (les centres des pixels), et hx et hy les dimension du pixel selon les axes correspondant. Si on ajoute un point au centre du rectangle, ce qui correspond au point commun aux quatres pixels (en utilisant la moyenne des valeurs des pixels), on forme quatre triangles et l'aire de la surface peut être approximée par la somme de leurs aires. On obtient les formules suivantes pour l'aire d'un triangle (en haut) et l'aire d'un pixel (en bas) :
La méthode est correctement définie pour les pixels intérieurs de la région analysée. Chacune des valeurs participe à huit triangles, deux pour chacune des quatre valeurs voisines. La moitié de chacun de ces triangles se trouve sur un pixel, l'autre moitié sur un autre pixel. En comptabilisant l'aire présente sur chaque pixel, l'aire totale est aussi définie pour les grains et les zones masquées. Il reste maintenant à définir l'aire pout les pixels du bord du champ de donné. Cette opération est étendant virtuellement l'image par une copie des pixels de bord sur chaque côté, rendant ainsi tous les pixels de l'image initiale à l'intérieur de la zone d'intérêt.
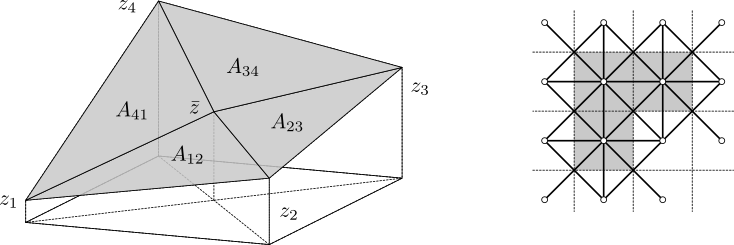
Schéma de triangulation pour le calcul d'aire (à gauche). Application de ce schéma sur un zone marquée de trois pixels (à droite), un grain par exemple. Les petits cercles représentes les vertex zi des centres des pixels, les lignes en pointillés représentent les bords des pixels, tandis que les lignes continues matérialisent la triangulation. L'aire estimée est ici égale à l'aire couverte par le masque (en gris).
Les fonctions statistiques uni-dimensionnelles sont accessibles en utilisant l'outil fonctions statistiques. L'outil vous permet de sélectionner la fonction à évaluer en utilisant la liste déroulante sur la gauche de la fenêtre. La prévisualisation du graphe est automatiquement rafraîchie. Vous pouvez sélectionner la direction à analyser (horizontale ou verticale), mais là encore il est préférable d'utiliser la direction du balayage rapide. Vous pouvez aussi choisir la méthode d'interpolation à utiliser. Une fois les réglages réalisés, vous pouvez cliquer sur pour fermer la fenêtre de l'outil et obtenir une nouvelle fenêtre de graphe contenant les données statistiques.
Astuce
De la même manière que l'outil statistiques, cet outil évalue par défaut les fonctions sur l'image entière, mais vous pouvez là aussi sélectionner une région de l'image.Les distributions des hauteurs et des pentes sont les fonctions les plus simples. Elles peuvent être calculées de manière non cumulative (i.e les densités), ou cumulative. Ces fonctions sont calculées sous forme d'histogrammes normalisés des hauteurs ou des pentes (obtenues à partir des dérivées selon la direction sélectionnée – horizontale ou verticale). En d'autres termes, les valeurs données en abscisse pour la « distribution angulaire » correspondent aux tangentes des angles, et non aux angles eux-mêmes.
La normalisation des densités ρ(p) (où p est la quantité correspondante, la hauteur ou la pente) est telle que
Bien évidemment, l'échelle des valeurs est alors indépendante du nombre de points et du nombre de classes de l'histogramme. Les distributions cumulatives correspondent aux intégrales des densités et leurs valeurs sont dans l'intervalle [0, 1].
Les distributions des hauteurs et des pentes sont des quantités statistiques de premier ordre, elles ne décrivent que les propriétés statistiques des points individuels. Pour un description complète des propriétés de la surface il est nécessaire d'étudier des fonctions d'ordre supérieur. On emploie en général des quantités statistiques de second ordre donnant les relations mututlles entre deux points de la surface. On trouve parmi ces quantités la fonction d'autocorrélation, la fonction de corrélation hauteur-hauteur et la densité spectrale de puissance. Une description de chacune de ces fonctions est donnée ci-dessous :
La fonction d'autocorrélation est donnée par
où z1 et z2 sont les valeurs des hauteurs aux points (x1, y1), (x2, y2) ; on a de plus, τx = x1 − x2 et τy = y1 − y2. La fonction w(z1, z2, τx, τy) décrit la densité de probabilité bi-dimensionnelle de la fonction aléatoire ξ(x, y) correspondant aux points (x1, y1), (x2, y2), et la distance entre ces points τ.
On peut évaluer cette fonction à partir de données AFM discrètes avec
où m = τx/Δx, n = τy/Δy. La fonction peut ainsi être évaluée par une série de valeurs discrètes τx et τy séparées respectivement par les intervalles d'échantillonnage Δx et Δy. La fonction d'autocorrélation bi-dimensionnelle peut peut être lancée par → → . Notez que, contrairement au cas uni-dimensionnel, les données sont censées avoir été mises à niveau au préalable, avec un niveau zéro correctement défini. La fonction d' n'effectue aucune mise à niveau. Cela vous laisse plus de contrôle sur les données et peut s'avérer utile dans certains cas. Toutefois, si vous êtes plus intéressés par le meilleur contraste de l'ACF plutôt que des valeurs bien définies, vous serez certainement intéressés par l'utilisation de la fonction valeur moyenne à zéro au préalable.
Pour les mesures AFM, on évalue généralement la fonction d'autocorrélation uni-dimensionnelle basée uniquement sur les profils pris le long de l'axe rapide de balayage. On peut dès lors l'évaluer sur les données avec
La fonction d'autocorrélation uni-dimensionnelle est souvent de forme gaussienne, c'est-à-dire qu'elle peut être donnée par la relation suivante :
où σ correspond à l'écart quadratique des hauteurs et T correspond à la longueur d'autocorrélation.
Nous avons la relation suivante pour la fonction d'autocorrélation exponentielle :
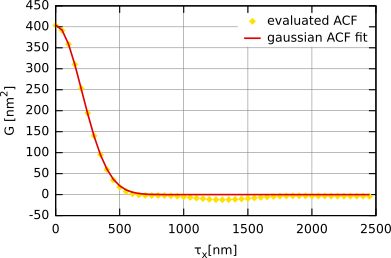
Fonction d'autocorrélation obtenue pour une surface aléatoire gaussienne artificielle (c'est-à-dire avec ayant une fonction d'autocorrélation gaussienne) avec σ ≈ 20 nm et T ≈ 300 nm.
On peut aussi présenter la fonction d'aucorrélation radiale Gr(τ), c'est-à-dire la fonction d'autocorrélation bi-dimensionnelle moyennée angulairement, qui contient évidemment la même information que la fonction d'autocorrélation uni-dimensionnelle pour les surfaces isotropes :
Note
Concernant les mesures optique (la spectroscopie à interférence réflectométrique ou l'ellipsométrie par exemple) la fonction d'autocorrélation gaussienne concorde généralement assez bien avec les propriétés de la surface. Toutefois certains articles traitant de la croissance ou de l'oxydation de surfaces postulent que la forme exponentielle est plus fidèle à la réalité.La différence entre la fonction de corrélation hauteur-hauteur et la fonction d'autocorrélation est très mince. Comme pour la fonction d'autocorrélation, on somme le produit de deux valeurs. Pour la fonction d'autocorrélation ces valeurs représentent les distances entre les points. Dans le cas de la fonction de corrélation hauteur-hauteur, on utilise le carré des différences entre les points.
Dans le cas des mesures AFM on évalue généralement la fonction de corrélation hauteur-hauteur uni-dimensionnelle basée sur les profils pris le long d'axe rapide de balayage. On peut dès lors l'évaluer sur les données avec
où m = τx/Δx. La fonction peut ainsi être évaluée par une série de valeurs discrètes τx séparées par l'intervalle d'échantillonnage Δx.
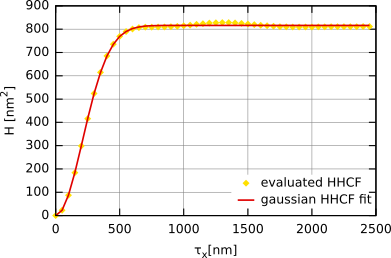
La fonction de corrélation hauteur-hauteur uni-dimensionnelle est souvent de forme gaussienne, c'est-à-dire qu'elle peut être donnée par la relation suivante :
où σ est l'écart quadratique des hauteurs et T est la longueur d'autocorrélation.
Nous avons la relation suivante pour la fonction de corrélation hauteur-hauteur exponentielle :
La figure suivante donne la fonction de corrélation hauteur-hauteur obtenue pour une surface gaussienne simulée. Elle est ajustée à l'aide de la formule donnée plus haut. Les valeurs résultantes de σ et T obtenues par l'ajustement de la fonction de corrélation hauteur-hauteur sont pratiquement identiques à celles de la fonction d'autocorrélation.
La densité spectrale de puissance bi-dimensionnelle correspond à la transformée de Fourier de la fonction d'autocorrélation
Comme pour la fonction d'autocorrélation, on évalue généralement la densité spectrale de puissance uni-dimensionnelle, donnée par l'équation
Cette fonction peut être calculée à l'aide d'une transforme de Fourier rapide (FFT) de la manière suivante :
où Pj(Kx) est le coefficient de Fourier de la j-ième ligne, c'est-à-dire
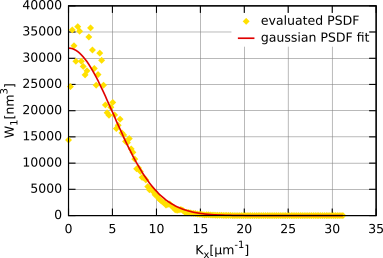
Si nous choisissons la fonction d'autocorrélation gaussienne, la relation gaussienne correspondante pour la PSD est
Pour une surface ayant une fonction d'autocorrélation exponentielle nous avons
La figure qui suit donne la PSD et son ajustement pour la même surface que celle utilisée pour la fonction d'autocorrélation et la fonction de corrélation hauteur-hauteur. On peut constater que la fonction peut là aussi être ajustée par une PSD gaussienne. Les valeurs résultantes de σ et T sont pratiquement identiques à celles obtenues pour l'ajustement de la fonction d'autocorrélation et la fonction de corrélation hauteur-hauteur.
On peut de même appliquer la PSD radiale Wr(K), c'est-à-dire la PSD bi-dimensionnelle intégrée angulairement, qui contient les mêmes informations que la PSD uni-dimensionnelle pour les surfaces isotropes :
Pour une surface ayant une fonction d'autocorrélation gaussienne, cette fonction est exprimée par
alors que pour une fonction d'autocorrélation exponentielle nous avons
Astuce
Gwyddion vous permet d'ajuster toutes les fonctions statistiques présentées ici par leurs formes gaussienne et exponentielle. Il suffit de cliquer sur dans la fenêtre de l'outil fonctions statistique. Cela créera une nouvelle fenêtre de graphe. Après avoir sélectionné celle-ci, cliquez sur → .Les fonctions de Minkowski permettent de décrire les caractéristiques géométriques globales de structures. Les caractéristiques bi-dimensionnelles discrètes de volume V, de surface S et de connectivité (caractéristique d'Euler-Poincaré) χ sont calculées à l'aide des formules suivantes :
Où N correspond au nombre total de pixels, Nblanc au nombre de pixels « blancs », c'est-à-dire au-dessus du seuil. Les pixels en-dessous du seuil sont considérés comme étant « noirs ». Le symbole Nlimite correspond au nombre de délimitations blanc-noir. Pour finir, Cblanc et Cnoir correspondent aux nombres de groupes continus de pixels respectivement blancs et noirs.
Dans le cas d'une image ayant des ensembles de valeurs continus les fonctions sont paramétrées par le seuil de hauteur ϑ qui sépare pixels blancs des pixels noirs, c'est-à-dire qu'on peut les voir comme des fonctions de ce paramètre. Et ce sont les fonctions V(ϑ), S(ϑ) et χ(ϑ) qui sont affichées.
La distribution de plage affiche la croissance de la plage de valeur en fonction de la distance latérale. Il s'agit toujours d'une fonction non décroissante.
Pour chaque pixel dans l'image, et chaque distance latérale, il est possible de calculer le minimum et le maximum parmi les valeurs des pixels situés à une distance inférieure à la distance donnée du pixel. La plage locale correspond à la différence entre ce maximum et ce minimum (et peut être visualisée en deux dimensions à l'aide la transformée de rang, dans la section des présentations). La moyenne des plages locales pour la totalité de l'image donne la courbe de plage.
Cet outil calcule les caractéristiques de chaque ligne ou colonne et les affiche en fonction de leur position. Cet outil est complémentaire de l'outil fonctions statistiques. Les caractéristiques disponibles sont les suivantes :
- Valeur moyenne, minimale, maximale et médiane.
- Valeur RMS des irrégularités de hauteur calculée à partir de la variance Rq.
- Asymétrie et kurtosis de la distribution des hauteurs.
- Longueur le long de la surface. Celle-ci est estimée en prenant la longueur totale des segments joignant les valeurs de hauteur dans la ligne ou la colonne.
- Pente globale, c'est-à-dire la tangente de la droite moyenne ajustée sur la ligne ou la colonne.
- Tangente β0. Il s'agit de la raideur des pentes locales, fortement liée au comportement des fonctions d'autocorrélation et de corrélation hauteur-hauteur autour de zéro. Dans le cas de valeurs discrètes on la calcule de la manière suivante :
- Paramètres de rugosité standards Ra, Rz, Rt.
En complément du graphe, la valeur moyenne et l'écart type de la quantité sélectionnée sont calculés à partir des valeurs obtenues pour les lignes ou les colonnes. À noter que l'écart type de la quantité sélectionnée représente la dispersion des valeurs des lignes ou colonnes individuelles, à ne pas interpréter comme l'erreur de la quantité bi-dimensionnelle équivalente.
Plusieurs fonctions du menu → concernent les statistiques des pentes (dérivées) bi-dimensionnelles.
La calcule simplement la distribution bi-dimensionnelle des dérivées, les coordonnées verticales et horizontales de l'image résultante sont respectivement les dérivées verticales et horizontales. Les pentes peuvent être calculées localement (en se basant sur un seul côté en bord d'image), ou si l'option utiliser l'ajustement du plan local est activée, en ajustant un plan sur les pixels environnants et en utilisant les gradients de celui-ci.
La peut aussi afficher des graphes représentant les distributions uni-dimensionnelles de quantités aux pentes locales et aux angles d'inclinaison des facettes donnés par la formule suivante :
Trois types de graphes sont disponibles :
- L', c'est-à-dire la distribution de l'angle d'inclinaison ϑ par rapport au plan horizontal. La représentation de la pente sous forme d'angle nécessite bien évidemment que les valeurs et dimensions représentent la même quantité physique.
- L' est similaire au graphe de ϑ, excepté que l'on affiche la distribution de la dérivée v au lieu de l'angle.
- L' affiche l'intégrale de v2 pour chaque direction φ dans le plan horizontal. Cela signifie qu'il ne s'agit d'une simple distribution de φ car les zones présentant des pentes élevées contribuent plus que les zones planes.
La est un outil de visualisation qui ne calcule pas une distribution au sens strict du terme. Pour chaque dérivée v, elle affiche le cercle de points satisfaisant
Le nombre de points sur le cercle est donné par le nombre de pas.
Les paramètres de structures bi-dimensionnelles régulières peuvent être obtenus en analysant les données transformées en une figure affichant leur régularité. la fonction d'auto-corrélation (ACF) et la densité spectrale de puissance (PSDF) sont particulièrement bien adaptés à cette tâche car elles présentent des pics correspondant aux vecteurs du réseau de Bravais formés par le motif périodique.
Les pics de l'ACF bi-dimensionnelle correspondent aux vecteurs de maille dans l'espace direct (ainsi que leurs multiples entiers et leurs combinaisons linéaires). Les pics de la PSDF bi-dimensionnelle correspondent aux vecteurs de la maille inverse. Les matrices formées les vecteurs de maille dans l'espace direct et dans l'espace des fréquences sont les transposées inverses l'une de l'autre. Avec une transformation adéquate, l'une et l'autre peuvent être utilisées pour mesurer la maille.
La fonction → → permet d'utiliser l'ACF ou la PSDF pour effectuer cette mesure. Comme les mailles à large période correspondent à des pics éloignés dans l'ACF et proches dans la PSDF, il est préférable d'utiliser l'ACF dans ce type de situation pour améliorer la résolution. À l'inverse, la PSDF est plus adaptée dans le cas où la période de la maille est petite. La boîte de dialogue vous permet de passer librement de la représentation dans l'espace direct ou l'espace des fréquences, la maille sélectionnée étant transformée en conséquence.
Le bouton tente de déterminer automatiquement la maille de l'image. S'il ne sélectionne pas les vecteurs que vous souhaitez, vous pouvez les ajuster manuellement dans l'image. La sélection peut se faire de manière similaire à la distorsion affine (cela revient à choisir afficher la maille sous forme de maille), ou afficher et ajuster uniquement les deux vecteurs (vecteurs). Dans les deux cas, lorsque vous choisissez la position approximative des pics, le bouton permet d'ajuster la position des vecteurs afin d'améliorer la correpondance avec les pics. Le bouton peut être utilisé pour remettre les vecteurs à dans un état initial sain.
Les paramètres des vecteurs de maille sont toujours donnés dans l'espace direct, avec leurs composantes, leurs longueurs totales et leurs directions. L'angle φ correspond à celui entre les deux vecteurs.
→ →
L'analyse des facettes permet d'étudier de manière interactive l'orientation des facettes présentes dans les données, et de marquer les facettes ayant des orientations spécifiques sur l'image. La vue de gauche affiche les données avec une prévisualisation des facettes marquées. La vue de droite, que l'on appellera par la suite le visualisateur de facettes, affiche la distribution bi-dimensionnelle des pentes.
Le centre du visualisateur de facettes correspond toujours à une inclinaison nulle (facettes horizontales), la pente selon la direction x augmente vers la droite et la gauche, et la pente selon la direction y augmente vers les bords haut et bas. Le système de coordonnées exact est un peu complexe, il s'adapte à la plage de pentes présentes dans les données affichées.
La taille des facettes contrôle le rayon du plan ajusté localement à chaque point pour déterminer l'inclinaison locale. La valeur 0 signifie qu'aucun ajustement n'est réalisé, l'inclinaison locale est déterminée à partir des dérivées symétriques en x et y en chaque point. Le choix de la taille de voisinage est cruciale pour obtenir des résultats corects : elle doit être plus petite que les détails auxquels on s'intéresse pour éviter leur filtrage, tout en étant suffisamment grande pour éliminer le bruit présent dans l'imaage.
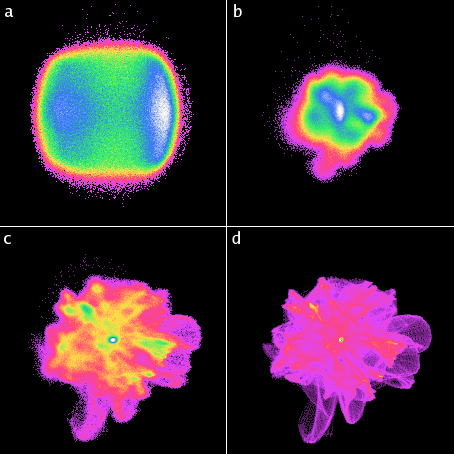
Illustration de influence de la taille du plan ajusté sur la distribution d'un scan fortement bruité d'une surface DLC délaminée. On peut constater que la distribution est complètement noyée dans le bruit pour les petites tailles de plan. Les valeurs de voisinage sont : (a) 0, (b) 2, (c) 4, (d) 7. Les plages d'angle et de couleur sont appliquées sur la dynamique complète de l'image, c'est-à-dire qu'elles varient d'une image à une autre.
La vue des données et le visualisateur de facettes permettent de sélectionner un point avec la souris et lire l'inclinaison de la normale à la facette correspondante ϑ et la direction φ sous Normale. Lorsque vous sélectionnez un point sur la vue des données, la sélection du visualisateur de facette est mise à jour pour afficher l'inclinaison sur ce point.
Le bouton ajuste la sélection du visualisateur de facette sur la maximum de la distribution des pentes (il s'agit de la position initiale de la sélection).
Le bouton met à jour le masque avec les zones ayant une pente similaire à la pente sélectionnée. Plus précisément, les zones ayant une pente dans la Tolérance de la pente sélectionnée. Le visualisateur de facettes affiche alors l'ensemble des pentes correspondant aux points marqués (notez que cet ensemble peut ne pas être circulaire dans le visualisateur de facettes, mais il ne s'agit que d'un effet de projection). L'inclinaison moyenne de tous les points dans la plage de pentes sélectionnée est affichée sous Normale Moyenne.
→ →
L'outil statistiques peut afficher une estimation de l'entropie différentielle de la distribution des valeurs. Il permet aussi d'estimer l'entropie différentielle de la distribution des pentes, et aide à visualiser la manière dont elle est calculée.
L'entropie différentielle de Shannon pour une fonction de densité de probabilité peut être exprimée par
où X est le domaine de la variable x. Par exemple, pour la distribution des hauteurs, x représente la hauteur de la surface, et X est l'axe réel complet. Pour la distribution des pentes, x est un vecteur à deux composantes donnant les dérivées selon les axes, et X est le plan correspondant.
Il existe de nombreuses méthodes plus ou moins sopĥistiquées d'estimation de l'entropie. Gwyddion utilise une méthode relativement simple basée sur l'histogramme dans laquelle la formule présentée plus haut est approximée par
, où pi et wi sont la densité de probabilité estimée, c'est-à-dire l'histogramme normalisé, et la largeur de la i-ème catégorie de l'histogramme.
Bien entendu, la valeur de l'entropie estimée dépend du choix de la largeur des catégories de l'histogramme – en dehors du cas de la distribution uniforme, pour laquelle l'estimation ne dépend pas de cette largeur. À partir de ce constat, on peut considérer que pour une distribution raisonnable, une largeur de catégorie adéquate est telle que l'entropie estimée ne varie pas lorsque l'on modifie cette largeur. Il s'agit du critère utilisé pour déterminer la largeur de catégorie la plus appropriée.
En pratique, cela signifie que l'entropie est estimée sur une large plage de largeur de catégorie (typiquement sur plusieurs ordres de grandeur). On obtien alors la courbe d'échelle affichée dans le graphe sur la droite de la fenêtre de dialogue. L'entropie est alors estimée en déterminant le point d'inflexion de la courbe. Dans le cas où aucun point d'inflexion ne serait présent, ce qui peut par exemple arriver dans le cas d'une distribution proche d'une somme de fonctions δ, alors l'entropie affichée sera une valeur largement négative.
Les entropies affichées sont sans unité car il s'agit de quantités logarithmiques. Notez qu'en cas de comparaison avec d'autres calculs, Gwyddion effectue toujours ce calcul en unités SI (par exemple en mètres et non en nanomètres) et le logarithme naturel est utilisé. La valeur est ainsi en unité naturelle d'information (nat).
L'entropie absolue dépend de la largeur absolue de la distribution. Par exemple, deux distributions gaussiennes de hauteurs ayant une valeur RMS différente auront une entropie différente. Ceci peut être utile lorsque l'on souhaite comparer la finesse absolue de structures dans la distribution des hauteurs. Inversement, il peut aussi être utile de les comparer indépendamment de leur échelle globale. Dans ce cas on peut utiliser le fait que la distributiokn gaussienne possède l'entropie maximale parmi toutes les distributions ayant la même valeur RMS. La différence entre cette valeur maximale et l'entropie estimée est appelée déficit d'entropie. Elle est positive par définition (sauf en cas de problème numérique).