La lecture de valeur et les opérations géométriques basiques constituent la base de tout logiciel de traitement de données. Gwyddion propose un large choix de fonctions pour mettre à l'échelle, tourner, ré-échantillonner ou extraire un profil des données. Cette section décrit ces fonctions, certes simples, mais essentielles.
La plupart des opérations de base sont accessibles dans le menu → ; certaines sont aussi gérées par les outils.
Ce groupe de transformations géométrique conserve les pixels, ce qui signifie qu'un pixel dans l'image transformée correspond exactement à un pixel dans l'image de départ. Il n'y a aucune interpolation.
Renversement des données horizontalement (c'est-à-dire autour de l'axe vertical), verticalement (autour de l'axe horizontal) ou de part et d'autre de la diagonale (échange des lignes et des colonnes) avec → → , ou , respectivement.
La rotation des données par multiples de 90 degrés est possible en utilisant les fonctions de rotation : → → , ou . Renverser selon les deux axes permet aussi de faire une rotation de 180°.
L'outil rognage permet de recadrer une image soit directement sur les données soit en mettant le résultat dans un nouveau canal (avec l'option Créer un nouveau canal). En activant l'option Conserver les décalages latéraux, les coordonnées du coin en haut à gauche de l'image résultante corresponderont à celles du coin en haut à gauche de la sélection, dans le cas contraire les coordonnées seront mises à (0, 0).
→ → .
L'extension correspond à l'opération inverse du rognage. Bien évidemment, il n'est possible d'ajouter des données réelles sur les bords qu'en mesurant des données supplémentaires. Cette fonction propose donc à la place des méthodes d'extension artificielles telles que la prolongation périodique ou la répétition des valeurs des bords de l'image. La méthode de Laplace fonctionne de manière identique à l'interpolation des données sous le masque et crée une extension lisse convergeant vers la valeur moyenne du bord complet de l'image.
Ce groupe de transformations ne conserve pas la relation pixel à pixel, elles nécessitent une interpolation.
→ →
Ré-échantillonne les données vers de nouvelles dimensions des pixels (nombre de lignes et de colonnes de l'image) à l'aide de la méthode d'interpolation sélectionnée. Les dimensions physiques sont conservées.
Si vous souhaitez plutôt spécifier les dimensions physiques des pixels, utilisez la fonction Ré-échantillonner.
→ →
Sur-échantillonne les données (le long de l'axe ayant les plus gros pixels) de manière à rendre les pixels carrés. La plupart des scans ont un rapport d'aspect de 1:1, cette fonction n'aura aucun effet sur ceux-ci.
→ →
Ré-échantillonnage des données vers une nouvelle taille de pixels en utilisant la méthode d' interpolation sélectionnée. La taille de pixel peut être choisie pour correspondre à celle d'une autre image, ce qui est nécessaire pour les opérations multi-données. Les dimensions physiques restent inchangées.
Si vous souhaitez plutôt spécifier le nombre de lignes, de colonnes ou le rapport d'échelle de l'image, utiliser la fonction échelle.
La fonction → → tourne l'image selon un angle arbitraire. Contrairement aux transformations géométriques simples citées plus haut, cette fonction nécessite une interpolation, qui peut être définie dans la fenêtre de dialogue.
Après rotation, l'image n'est plus un rectangle dont les côtés sont parallèles aux axes. L'option Taille résultante permet de définir la zone à considérer pour l'image finale :
- Identique à l'original conserve la taille de l'image, coupant certaines données et ajoutant des valeurs dans les parties externes.
- Étendre aux données complètes évite de couper certaines données de l'image – ce qui aboutit à plus de données ajoutées dans les parties externes.
- Couper aux données valides empêche l'ajout de valeur dans les parties externes – ce qui revient à tronquer plus ou moins fortement l'image.
Un masque peut être ajouté au-dessus des pixels correspondant à l'extérieur de l'image originale.
→ →
Le regroupement (« binning ») est une autre méthode de réduction de la taille de l'image. Le résultat n'est pas créé en interpolant les pixels, mais en les moyennant pour obtenir chaque nouveau pixel.
Le bloc rectangulaire de pixels à moyenné correspond au regroupement. Vous pouvez contrôler sa largeur et sa hauteur, qui correspondent aussi aux facteurs de ré-échantillonnage dans chaque direction. L'origine du premier bloc peut être décalé par rapport à l'origine de l'image. Notez toutefois que l'image résultante n'est formée que de blocs complets ; les blocs incomplets en bord d'image sont ignorés.
On peut utiliser la moyenne tronquée en lieu et place de la moyenne habituelle, les paramètres Tronquer les plus bas et Tronquer les plus hauts contrôlant le nombre de valeurs les plus basses ou les plus hautes sont ignorées dans le calcul de la moyenn. Cette fonction peut être utile pour éliminer les pixels aberrants. Lorsque l'option Sommer au lieu de moyenner est activée, la valeur résultante correspond à la somme des contributions. Cette option n'a que peu de sens pour des données topographiques habituelles. Toutefois, si l'image représente une donnée de type densité, dont l'intégrale doit être conservée, alors la sommation correspond à la bonne opération.
Ce groupe de fonctions conserve la correspondance pixel à pixel, et ne modifie que leur valeur. Le module Arithmétique permet aussi de manipuler les données à l'aide d'expression arithmétiques.
→ → .
Cette fonction inverse les données par rapport à la valeur moyenne, celle-ci est donc conservée.
→ → .
La plage des valeurs peut être limitée en coupant les valeurs en dehors de la plage spécifiée. La plage peut être ajustée manuellement ou à partir de la plage de fausses couleurs définie précédemment avec l'outil plage de couleurs, il est aussi possible de supprimer les points aberrants en dehors d'un multiple arbitraire du RMS à partir de la valeur moyenne.
→ → .
Les données périodiques, telles que les angles, sont parfois enregitrées avec une mauvaise valeur de repli, ce qui les fait apparaître discontinues. Par exemple, la plage d'angles va de 0 à 360 degrés, mais les données pourraient être continues si elles s'étalaient de −180 à 180 degrés. Un simple changement de la valeur de repli permet de retrouver la continuité.
La fonction propose deux paramètres. La Plage est l'étendue des valeurs (période selon la direction z). Le Décalage spécifie la valeur de séparation pour le repli. La formule exacte est :
Les symboles r et Δ représentent respectivement la plage et le décalage. La fonction fmod est le modulo (reste) à virgule flottante.
→ → .
Change les dimensions physiques, les unités ou l'échelle, ainsi que les décalages latéraux. Cette fonction est très utile lorsque des données brutes ont été importées avec des échelles erronées ou tout simplement pour recalibrer les dimensions et les valeurs.
Note
Les réglages sont enregistrés à chaque utilisation de cette fonction. Cela permet de répéter les mêmes calibrations sur différentes données. Cela peut aussi facilement aboutir à appliquer une calibration d'une action précédente alors que vous ne le souhaitez pas. En cas de doute commencez par presser le bouton pour effacer tous les décalages et facteurs de calibration.La méthode la plus simple pour lire une valeur est de placer le curseur de la souris sur le point dont on veut connaître la valeur. Les coordonnées et/ou la valeur sont alors affichées dans la barre d'état de la fenêtre de données ou la la fenêtre de graphe.
L'outil de lecture de valeur offre plus de possibilités : il affiche les coordonnées et valeurs du dernier point de la fenêtre de données sur lequel le bouton de souris a été cliqué. Il affiche une vue agrandie de l'image autour de ce point.
L'outil peut moyenner la valeur sur une zone circulaire centrée sur ce point, ce que l'on peut contrôler avec l'option Rayon de moyennage. Lorsque le rayon vaut 1, la valeur du pixel seul est affichée. Le bouton ajuste la surface de manière à ce que le z courant devienne le nouveau niveau zéro.
L'outil Lecture de valeur peut aussi afficher l'inclinaison de la facette locale ou la courbure de surface locale. Là encore, le Rayon de moyennage détermine le rayon de l'aire à utiliser pour ajuster le plan local. Le calcul de courbure en particulier à besoin d'une zone relativement large pour être fiable.
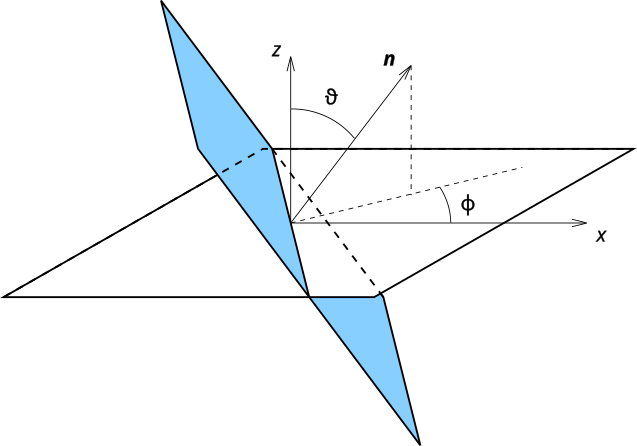
Dans tous les outils de Gwyddion, les inclinaisons de facette et de plan sont donnés sous la forme des coordonnées sphériques (ϑ, φ) du vecteur normal au plan.
L'angle ϑ est l'angle entre la direction verticale et la normale, ce qui veut dire que ϑ = 0 pour des facettes horizontales, et qu'il augmente avec la pente. Sa valeur est toujours positive.
L'angle φ est l'angle direct entre l'axe x et la projection de la normale sur le plan xy, comme le montre la figure ci-dessous. Dans le cas des facettes, cela signifie que φ correspond à la direction de la pente descendante de la facette.
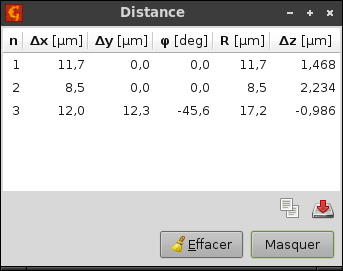
Les distances et différences de hauteur peuvent être mesurées avec l'outil distance. Il affiche les distances horizontale (Δx), verticale (Δy) et totale (R) ; l'azimuth φ (mesurée de la même manière que l'inclinaison φ ) et la différence de hauteur du point final Δz pour un ensemble de lignes sélectionnées sur les données.
Les distances peuvent être copiées dans le presse-papier ou sauvegardées dans un fichier texte à l'aide des boutons situés sous la liste.
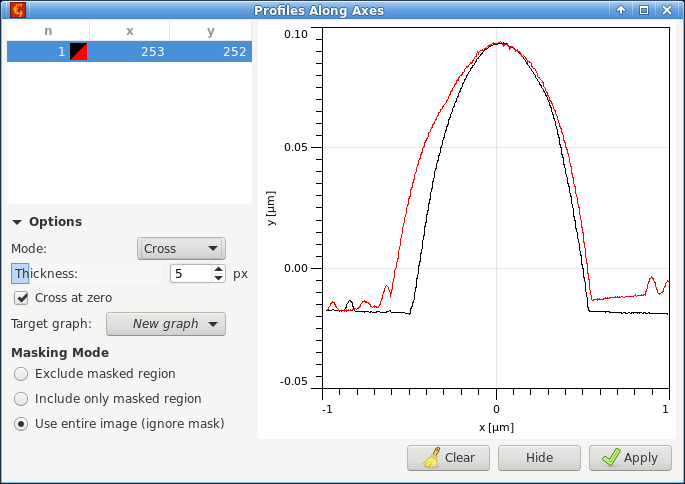
L'outil Profils le long des axes extrait des lignes de scan selon les directions horizontale et/ou vertical. La direction peut être contrôlé par l'option Mode, qui peut être Horizontal, Vertical ou Croix. Dans le mode croix, les deux profils sont extraits simultanément.
Lorsque l'option Coupure à zéro est activée, l'origine des abscisses correspond au point de croissement des profils (ou bien à la marque sur l'axe pour des profils verticaux ou horizontaux). Cette option est utile pour aligner plusieurs profils sur un même graphe. Si celle-ci est désactivée, les coordonnées du profil correspondent à celle de l'image dans cette même direction.
Les profils peuvent être de différentes « épaisseurs », ce qui signifie que plusieurs lignes de scan sont moyennées de part et d'autre de la direction sélectionnée. Cette option est utile pour éliminer le bruit lors de la mesure d'un objet ayant un aspect régulier. La largeur du profil est visulisable sur l'image à l'aide des marqueurs de fin de ligne.
Les lignes de scan provenant de plusieurs images peuvent être vues simultanément à l'aide la fonction Multi-profils.
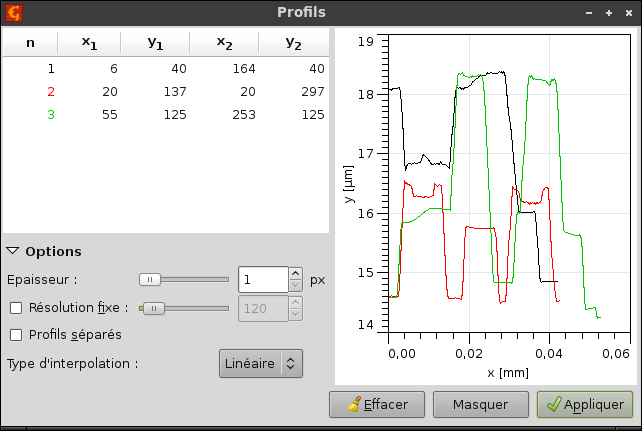
L'outil profils extrait des profils le long de lignes arbitraires, dessinés et ajustés sur l'image à l'aide de la souris, et les affiche en direct dans une fenêtre d'aperçu. Les profils peuvent être de différentes « épaisseurs », ce qui signifie que des pixels supplémentaires voisins perpendiculairement à la direction du profil sont utilisés pour évaluer un point donné du profil, et ce d'autant plus que l'épaisseur du profil est grande. Cette option peut être très utile pour s'affranchir du bruit lors de la mesure d'un objet ayant une forme régulière. L'épaisseur du profil est indiqué sur l'image à l'aide des marqueurs de fin de ligne.
Après avoir sélectionné les profils, ceux-ci peuvent être extraits sous forme de graphes (séparés ou groupés dans une fenêtre de graphes) pour pouvoir être ensuite analysées à l'aide des fonctions d'analyse des graphes.
La courbe du profil est construite à partir de données échantillonnées sur des intervalles réguliers le long de la ligne sélectionnée. Les valeurs des points ne tombant pas exactement sur le centre des pixels (ce qui est normalement le cas pour les lignes obliques) sont interpolées en utilisant la méthode d'interpolation choisie. A moins qu'un nombre explicite d'échantillons soit choisi à l'aide de l'option Résolution fixe, le nombre d'échantillons correspond à la longueur en pixels de la ligne. Ce qui signifie que pour les lignes parfaitement horizontales ou verticales aucune interpolation ne sera appliquée.
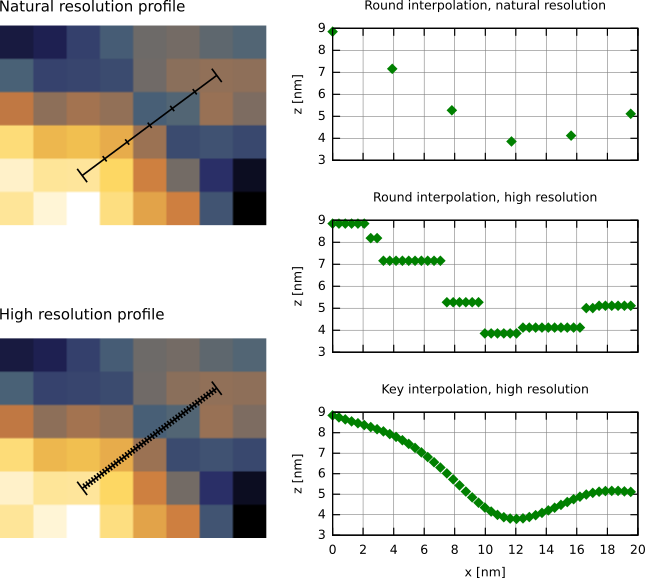
Illustration de l'échantillonnage du profil extrait d'une ligne oblique. Les figures sur la gauche montrent les points le long de la ligne pour laquelle les valeurs sont lues à la résolution naturlelle et à très haute résolution. Les graphes sur la droite montrent les valeurs extraites. La comparaison des profils à résolution haute et naturelle avec l'interpolation arrondie montre que les points de la courbe à la résolution naturelle sont en fait un sous-ensemble des points de la courbe à haute résolution. L'influence de la méthode d'interpolation sur les valeurs des points ne correspondant pas à la grille est démontrée par les deux graphes du bas, en comparant les interpolations arrondi et Key à haute résolution.
Lors de la mesure de profils de bords ou de marches, il est en général nécessaire de choisir une direction perpendiculaire au bord. Les boutons et peuvent aider dans cette tâche. Le premier bouton tente d'améliorer l'orthogonalité de la ligne en cours d'édition, tandis que le second tente d'améliorer toutes les lignes. Le centre des lignes est préservé, seule la direction des profils est modifiée. L'amélioration automatique n'est pas infaillible, mais elle fonctionne la plupart du temps correctement sur des bords relativement propres.
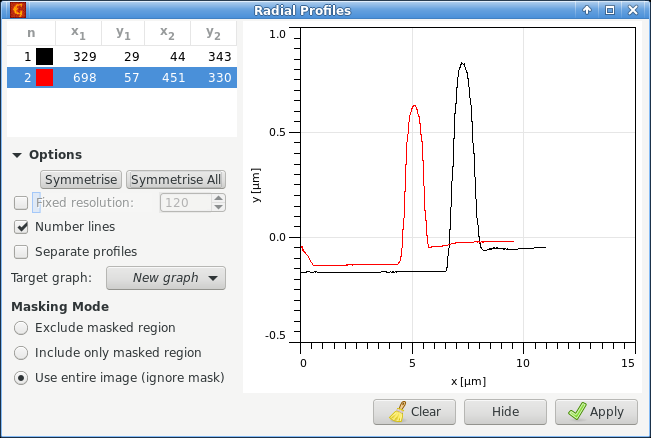
L'outil Profils radiaux est similaire à l'outil Profils. Il n'extrait toutefois pas de profils le long de lignes. La ligne dessinée est en fait utilisée pour définir une zone circulaire dont le centre est indiqué par une marque sur la ligne. Le profil extrait est ensuite obtenu par moyennage angulaire. Cette fonction est utile pour obtenir le profil de formes à symétrie de révolution. L'abscisse du graphe correspond alors à la distance depuis le centre au lieu de la position sur la ligne.
Bien que la ligne puisse être ajustée manuellement, il peut être difficile de trouver le meilleur centre pour les profils radiaux. L'outil peut donc tenter de localiser précisément le meilleur centre à utiliser. Il suffit juste de positionner approxiamtivement la ligne puis presser le bouton pour ajuster la ligne sélectionnée, ou le bouton or pour ajuster toutes les lignes. Les lignes seront alors légèrement décalées pour minimiser les différences entre les profils selon différentes directions depuis le centre.
La fonction → → crée des données volumiques à partir d'une image. Le champ de hauteur est considéré comme étant la surface d'un objet solide, ce qui est habituel dans le domaine de la microscopie à sonde. Les voxels situés sous la surface (dans la matière) sont remplis de 1, tandis que les voxels situés au-dessus (à l'extérieur) sont remplis de 0. La coordonnée z des données volumiques correspond donc aux valeurs de l'image, tandis que les valeurs des données volumiques n'ont aucune unité.
La fonction → → crée des données volumiques à partir d'une séquence d'images. Toutes les images du fichier doivent avoir les mêmes dimensions. Elles sont alors traitées comme des plans dans les données volumiques créées en accumulant les images. La coordonnée z des données volumiques correspondent donc à l'indice de la pile (il peut être spécifié dans la fenêtre de dialogue), tandis que les valeurs des données volumiques auront les mêmes unités que celles des images.
La fonction → → crée des données XYZ à partir d'une image. Chaque pixel de l'image correspond à un point dans les données XYZ générées. Les coordonnées xy forment donc une grille régulière et toutes les unités sont identiques à celles de l'image.
La fonction → → crée des données XYZ à partir de trois images, l'une contenant des coordonnées x, une autre des coordonnées y et la dernière des coordonnées z. Cette fonction peut être utile lorsque les données sont mesurées selon une grille régulière, mais que les positions effectives des mesures diffèrent d'une grille régulière, et que les coordonnées des points sont enregistrées dans d'autres canaux.