Les modules Présentation ne modifient pas les données, ils donnent les résultats sur une couche séparée affichée par-dessus les données originales. Les autres outils et modules de traitement des données continuent à opérer sur les données sous-jacentes. Pour supprimer une présentation il suffit de faire un clic droit sur la fenêtre des données, et sélectionner .
Le menu → propose les opérations basiques de présentation :
Attache un autre champ de données sous forme de présentation aux données courantes. Notez que cette option très utile peut prêter à confusion lorsqu'on évalue les propriétés des données, car celles-ci sont évaluées sur les données sous-jacentes (et non depuis celles de la présentation, même si celles-ci peuvent ressembler aux données).
Supprime la présentation de la fenêtre de données courante. Cette opération est une alternative au menu contextuel obtenu en faisant clic-droit dans la fenêtre des données.
Extrait la présentation de la fenêtre de données courante vers un nouveau canal placé dans le même fichier. On peut ainsi obtenir des données de présentation que l'on pourra traiter par la suite. Notez toutefois que les données extraites n'ont aucune échelle, car les présentations permettent en général de visualiser certaines informations, auxquelles il est difficile voire impossible d'assigner une quantité physique. La plage de valeur du nouveau canal est ainsi toujours [0, 1].
→ →
Fonction simple et très utile permettant de visualiser les données telles qu'elles le seraient en étant éclairées selon une direction donnée. Cette dernière peut être définie pas l'utilisateur. Il est aussi possible de mélanger l'image ombrée avec l'image originale pour des raisons de présentation. Bien évidemment, l'image résultante n'a aucune signification physique.
→ →
Les filtres des gradients Sobel et Prewitt (horizontaux et verticaux) créent des images similaires à celles obtenues avec la fonction Ombre, mais ici les données de sortie résultent de la convolution des données par des noyaux relativement standards. Elles peuvent donc être utilisées par la suite pour d'autres traitements par exemple. Les noyaux des filtres horizontaux sont donnés ci-dessous, les noyaux verticaux ne diffèrent que par une réflection autour de la diagonale principale.
→ →
On porte souvent un intérêt particulier dans la visualisation des discontinuités présentes dans l'image, en particulier celles de valeur (ordre zéro) et celles de dérivée (premier ordre). Bien que les méthodes de localisation des deux sont communément qualifiées de « détection de bord », celles-ci sont en fait assez différentes, nous ferons donc référence à la première comme détection de saut, et à la seconde comme détection de bord. Les méthodes de détection des détails plus spécifiques, par exemple les coins, sont aussi couramment utilisées, celles-ci sont généralement d'ordre zéro.
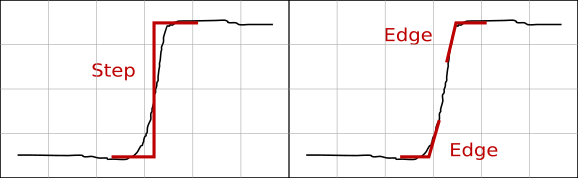
L'ordre d'une méthode de détection peut être visualisé facilement sur l'image obtenue, la détection de bord produisant typiquement des lignes doubles au niveau des discontinuités de valeur, tel qu'illustré dans l'image qui suit. Bien que les positions des bords haut et bas coïncident dans un saut idéal, les données d'un véritable saut contiennent en fait deux bords distincts, tel que l'illustre l'image. De plus, la détection de deux bords sur un saut de valeur est souvent un aspect inhérent des méthodes de détection de bord.
Les fonctions de détection de saut et de bord suivantes sont disponibles dans Gwyddion (les dernières sont plutôt expérimentales, mais elles donnent souvent de meilleurs résultats que les algorithmes les plus connus) :
- Canny
Le détecteur de bord Canny est très connu, il peut être utilisé pour extraire l'image des fortes discontinuités sous forme de fines lignes larges d'un pixel.
- Laplacien d'une gaussienne
Ce filtre est une simple convolution par le noyau suivant (il s'agit de la limite du laplacien discret d'un filtre gaussien pour σ → 0) :
- Coupure à zéro
La détection de bord par coupure à zéro marque les lignes où le résultat du filtre laplacien d'une gaussienne change de signe, c'est-à-dire lorsqu'il coupe zéro. La largeur à mi-hauteur (FWHM) de la gaussienne détermine le niveau de détail couvert par ce filtre. Le seuil permet d'exclure les changements de signe sur de trop petites valeurs absolues des pixels voisins, ce qui permet de filtrer le bruit. Notez toutefois que pour un seuil non nul les lignes de bord peuvent devenir discontinues.
- Saut
Algorithme de détection de saut donnant une bonne résolution, c'est-à-dire des lignes de discontinuités précises, ainsi qu'une bonne dynamique tout en étant relativement peu sensible au bruit. Le principe est assez simple : il visualise la racine de la différence entre les quantiles 2/3 et 1/3 des valeurs présentes dans un voisinage de 2,5 pixels de rayon centré autour de l'échantillon.
- RMS
Ce détecteur de saut visualise les zones ayant de fortes variations locales. Ce filtre calcule et affiche la moyenne quadratique des écarts à la moyenne dans un voisinage circulaire de 2,5 pixels de rayon centré sur chaque échantillon.
- Bord RMS
Cette fonction effectue essentiellement un post-traitement de la sortie RMS à l'aide d'un filtre similaire au laplacien afin de mettre en valeur les limites des zones ayant de fortes variations locales des valeurs. Malgré son nom, ce filtre est un détecteur de saut.
- Non-linéarité locale
Détecteur de bord permettant de visualiser les zones de non planéité locales. Il ajuste un plan sur un voisinage circulaire de 2,5 pixels de rayon centré sur chaque échantillon, puis calcule la somme quadratique résiduelle de cet ajustement réduit par la pente du plan, c'est-à-dire divisé par 1 + bx2 + by2 où bx et by sont respectivement les coefficients du plan dans les directions x et y. La racine carrée est finalement affichée.
- Inclinaison
Permet de visualiser l'angle d'inclinaison ϑ du plan local. Techniquement, cette fonction appartient aux détecteurs de saut, toutefois la mise en valeur des sauts n'est pas très forte et ce filtre est plutôt destiné à une comparaison visuelle des différentes pentes présentes dans l'image.

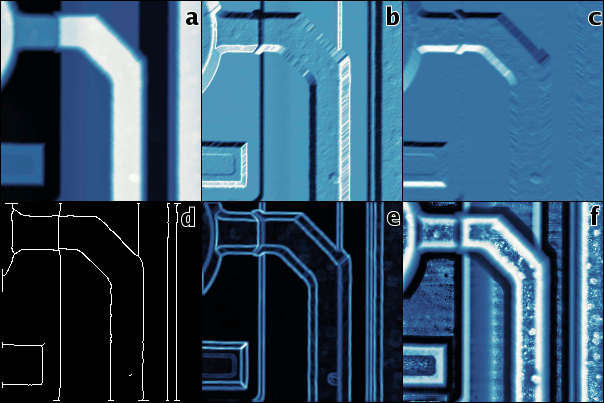
Comparaison des méthodes de détection de saut et de bord sur plusieurs exemples de données. Canny et coupure à zéro sont des détecteurs de saut produisant des lignes de bord d'un pixel de large, saut et inclinaison sont des détecteurs de saut donnant des données continues, non-linéarité locale est un détecteur de bord – la détection de bord est aisément observée sur les seconde et troisième lignes. Notez que la coupure à zéro est ajustable, ses paramètres ont été choisis de manière à produire des résultats intéressants pour chaque exemple.
→ →
Méthode permettant de visualiser les détails dans les zones présentant des variations aussi bien faibles qu'élevées. Le calcul détermine la plage de valeurs locale (ou variation) autour de chaque échantillon, et l'étire de manière à égaliser cette variation sur toutes les données.
→ →
Méthode alternative d'amélioration locale du contraste. Il s'agit d'un filtre égaliseur passe-haut, complémentaire du filtre médian. Chaque valeur de pixel est transformée en sa valeur de rang parmi toutes les valeurs dans un voisinage donné. Le rayon de voisinage est défini avec la taille du noyau.
L'effet net est que tous les maxima locaux sont égalisés à la même valeur maximale, tous les minima à la même valeur minimale, et toutes les valeurs n'étant un maximum ou un minimum sont transformées dans la plage définie en fonction de leur rang. Comme la sortie du filtre de rayon r contient au plus π(r + 1/2)2 valeurs différentes (approximativement), le filtre aboutit aussi à une discrétisation des valeurs, en particulier pour les noyaux de petite taille.
→ →
Cette fonction affiche un rendu similaire à une image SEM (Scanning Electron Microscope, microscope à balayage électronique) à partir d'une image topographique à l'aide d'une méthode de Monte-Carlo la plus simple possible. Pour chaque pixel de la surface un nombre de lignes partant de celui-ci sont choisies avec des directions aléatoires et une distribution gaussienne des longueurs. L'écart-type de la distribution est contrôlé par le paramètre rayon d'intégration. Si l'extrémité de la ligne reste dans le vide, la luminosité du pixel d'origine est augmentée. Si elle atteint de la matière, c'est-à-dire que la hauteur de la ligne se trouve sous la surface, alors la luminosité est diminuée. Il s'agit plus précisément de la description de la méthode Monte-Carlo. Le nombre de lignes est contrôlé par le paramètre qualité. De manière similaire, la même luminosité peut être calculée par l'intégration directe de tous les pixels présents dans un voisinage circulaire. Il s'agit alors de la méthode intégration.
Comme ce calcul plutôt simple peut tout de même prendre beaucoup de temps, il est utile de prendre en compte la dépendance entre la vitesse de calcul et les paramètres. Le temps de calcul de la méthode intégration ne dépend que du rayon d'intégration. Dans le cas de la méthode Monte-Carlo, le temps de calcul dépend essentiellement du paramètre qualité (il y a aussi une légère dépendance à la topographie locale).