Вейвлет-преобразование - преобразование, похожее на преобразование Фурье (или гораздо больше на оконное преобразование Фурье) с совершенно иной оценочной функцией. Основное различие лежит в следующем: преобразование Фурье раскладывает сигнал на составляющие в виде синусов и косинусов, т.е. функций, локализованных в Фурье-пространстве; напротив, вейвлет-преобразование использует функции, локализованные как в реальном, так и в в Фурье-пространстве. В общем, вейвлет-преобразование может быть выражено следующим уравнением:
где * - символ комплексной сопряженности и функция ψ - некоторая функция. Функция может быть выбрана произвольным образом, но она должна удовлетворять определённым правилам.
Как видно, вейвлет-преобразование на самом деле является бесконечным множеством различных преобразований в зависимости от оценочной функции, использованной для его расчёта. Это является основной причиной, почему термин «вейвлет-преобразование» используется в весьма различных ситуациях и для различных применений. Также существует множество типов классификации вариантов вейвлет-преобразования. Здесь мы покажем только деление, основанное на ортогональности вейвлетов. Можно использовать ортогональные вейвлеты для дискретного вейвлет-преобразования и неортогональные вейвлеты для непрерывного. Эти два вида преобразования обладают следующими свойствами:
- Дискретное вейвлет-преобразование возвращает вектор данных той же длины, что и входной. Обычно, даже в этом векторе многие данные почти равны нулю. Это соответствует факту, что он раскладывается на набор вейвлетов (функций), которые ортогональны к их параллельному переносу и масштабированию. Следовательно, мы раскладываем подобный сигнал на то же самое или меньшее число коэффициентов вейвлет-спектра, что и количество точек данных сигнала. Подобный вейвлет-спектр весьма хорош для обработки и сжатия сигналов, например, поскольку мы не получаем здесь избыточной информации.
- Непрерывное вейвлет-преобразование, напротив, возвращает массив на одно измерение больше входных данных. Для одномерных данных мы получаем изображение плоскости время-частота. Можно легко проследить изменение частот сигнала в течение его длительности и сравнивать этот спектр со спектрами других сигналов. Поскольку здесь используется неортогональный набор вейвлетов, данные высоко коррелированы и обладают большой избыточностью. Это помогает видеть результат в более близком человеческому восприятию виде.
Дополнительные подробности о вейвлет-преобразовании доступны на тысячах интернет-ресурсов о вейвлетах в сети, или, например, здесь [1].
В библиотеке обработки данных Gwyddion реализованы оба этих преобразования и использующие вейвлет-преобразование модули доступны в меню → .
Дискретное вейвлет-преобразование (DWT) - реализация вейвлет-преобразования с использованием дискретного набора масштабов и переносов вейвлета, подчиняющихся некоторым определённым правилам. Другими словами, это преобразование раскладывает сигнал на взаимно ортогональный набор вейвлетов, что является основным отличием от непрерывного вейвлет-преобразования (CWT), или его реализации для дискретных временных рядов, иногда называемой непрерывным вейвлет-преобразованием дискретного времени (DT-CWT).
Вейвлет может быть сконструирован из функции масштаба, которая описывает свойства его масштабируемости. Ограничение состоит в том, что функция масштаба должна быть ортогональна к своим дискретным преобразованиям, что подразумевает некоторые математические ограничения на них, которые везде упоминаются, т.е. уравнение гомотетии
где S - фактор масштаба (обычно выбирается как 2). Более того, площадь под функцией должна быть нормализована и функция масштабирования должна быть ортогональна к своим численным переносам, т.е.
После введения некоторых дополнительных условий (поскольку вышеупомянутые ограничения не приводят к единственному решению) мы можем получить результат всех этих уравнений, т.е. конечный набор коэффициентов ak которые определяют функцию масштабирования, а также вейвлет. Вейвлет получается из масштабирующей функции как N где N - чётное целое. Набор вейвлетов затем формирует ортонормированный базис, который мы используем для разложения сигнала. Следует отметить, что обычно только несколько коэффициентов ak будут ненулевыми, что упрощает расчёты.
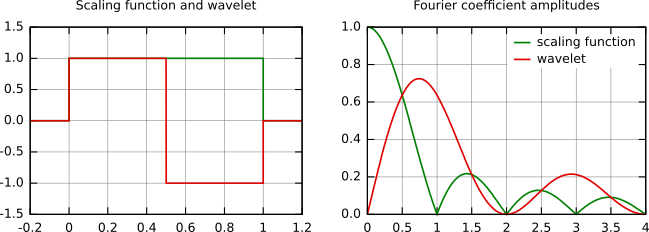
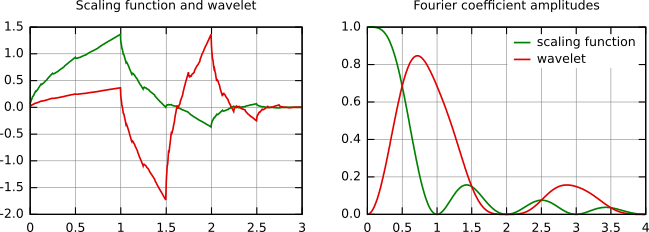
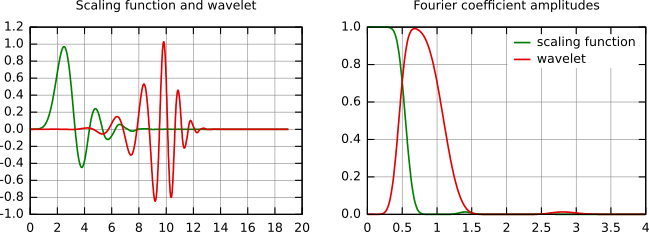
На следующем рисунке показаны некоторые масштабирующие функции и вейвлеты. Наиболее известным семейством ортонормированных вейвлетов явлется семейство Добеши. Её вейвлеты обычно обозначаются числом ненулевых коэффициентов ak, таким образом, мы обычно говорим о вейвлетах Добеши 4, Добеши 6, и т.п. Грубо говоря, с увеличением числа коэффициентов вейвлета функции становятся более гладкими. Это явно видно при сравнении вейвлетов Добеши 4 и 20, представленных ниже. Другой из упомянутых вейвлетов - простейший вейвлет Хаара, который использует прямоугольный импульс как масштабирующую функцию.
Существует несколько видов реализации алгоритма дискретного вейвлет-преобразования. Самый старый и наиболее известный – алгоритм Малла (пирамидальный). В этом алгоритме два фильтра – сглаживающий и несглаживающий составляются из коэффициентов вейвлета и эти фильтры рекуррентно применяются для получения данных для всех доступных масштабов. Если используется полный набор данных D = 2N и длина сигнала равна L, сначала рассчитываются данные D/2 для масштаба L/2N - 1, затем данные (D/2)/2 для масштаба L/2N - 2, … пока в конце не получится 2 элемента данных для масштаба L/2. Результатом работы этого алгоритма будет массив той же длины, что и входной, где данные обычно сортируются от наиболее крупных масштабов к наиболее мелким.
В Gwyddion для расчёта дискретного вейвлет-преобразования используется пирамидальный алгоритм. Дискретное вейвлет-преобразование в двумерном пространстве доступно в модуле DWT.
Дискретное вейвлет-преобразование может использоваться для простого и быстрого удаления шума с зашумлённого сигнала. Если мы возьмём только ограниченное число наиболее высоких коэффициентов спектра дискретного вейвлет-преобразования, и проведём обратное вейвлет-преобразование (с тем же базисом) мы можем получить сигнал более или менее очищенный от шума. Есть несколько способов как выбрать коэффициенты, которые нужно сохранить. В Gwyddion реализованы универсальный порог, адаптивный по масштабу порог [2] и адаптивный по масштабу и пространству порог [3]. Для определения порога в этих методах мы сперва определяем оценку дисперсии шума, заданную
где Yij соответствует всем коэффициентам наиболее высокого поддиапазона масштаба разложения (где, как предполагается, должна присутствовать большая часть шума). Или же дисперсия шума может быть получена независимым путём, например, как дисперсия сигнала АСМ, когда сканирование не идёт. Для наиболее высокого поддиапазона частот (универсальный порог) или для каждого поддиапазона (для адаптивного по масштабу порога) или для окружения каждого пикселя в поддиапазоне (для адаптивного по масштабу и пространству порога) дисперсия рассчитывается как
Значение порога считается в конечном виде как
где
Когда порог для заданного масштаба известен, мы можем удалить все коэффициенты меньше значения порога (жесткий порог) или мы можем уменьшит абсолютное значение этих коэффициентов на значение порога (мягкий порог).
Удаление шума DWT доступно в меню → → .
Непрерывное вейвлет-преобразование (CWT) - реализация вейвлет-преобразования с использованием произвольных масштабов и практически произвольных вейвлетов. Используемые вейвлеты не ортогональны и данные, полученные в ходе этого преобразования высоко коррелированы. Для дискретных временных последовательностей также можно использовать это преобразование, с ограничением что наименьшие переносы вейвлета должны быть равны дискретизации данных. Это иногда называется непрерывным вейвлет-преобразованием дискретного времени (DT-CWT) и это наиболее часто используемый метод расчёта CWT в реальных применениях.
В принципеЮ непрерывное вейвлет-преобразование работает используя напрямую определение вейвлет-преобразования, т.е. мы рассчитываем свёртку сигнала с масштабированным вейвлетом. Для каждого масштаба мы получаем этим способом набор той же длины N, что и входной сигнал. Используя M произвольно выбранных масштабов мы получаем поле N×M, которое напрямую представляет плоскость время-частота. Алгоритм, используемый для этого расчёта может быть основан на прямой свёртке или на свёртке посредством умножения в Фурье-пространстве (это иногда называется быстрым вейвлет-преобразованием).
Выбор вейвлета для использования в разложении на время-частоту является наиболее важной вещью. Этим выбором мы можем влиять на разрешение результата по времени и по частоте.Нельзя изменить этим путём основные характеристики вейвлет-преобразования (низкие частоты имеют хорошее разрешение по частотам и плохое по времени; высокие имеют плохое разрешение по частотам и хорошее по времени), но можно несколько увеличить общее разрешение по частотам или по времени. Это напрямую пропорционально ширине используемого вейвлета в реальном и Фурье-пространстве. Если, например, использовать вейвлет Морле (реальная часть – затухающая функция косинуса), то можно ожидать высокого разрешения по частотам, поскольку такой вейвлет очень хорошо локализован по частоте. наоборот, используя вейвлет Производная Гауссиана (DOG) мы получим хорошую локализацию по времени, но плохую по частоте.
Непрерывное вейвлет-преобразование реализовано в модуле CWT, который доступен в меню → → .
[1] Adhemar Bultheel: Learning to swim in a sea of wavelets. Bull. Belg. Math. Soc. Simon Stevin 2 (1995), 1-45, doi:10.36045/bbms/1103408773
[2] S. G. Chang, B. Yu, M. Vetterli: Adaptive wavelet thresholding for image denoising and compression. IEEE Trans. Image Processing 9 (2000) 1532–1536, doi:10.1109/83.862633
[3] S. G. Chang, B. Yu, M. Vetterli: Spatially adaptive wavelet thresholding with context modeling for image denoising. IEEE Trans. Image Processing 9 (2000) 1522–1531, doi:10.1109/83.862630