Модули презентаций не изменяют данные, вместо этого они выводят результат в отдельный слой, отображаемый поверх оригинальных данных. Прочие модули и инструменты работы с данными по прежнему будут оперировать с нижележащими данными. Чтобы удалить презентацию нужно нажать правую кнопку мыши в окне данных и выбрать в появившемся меню .
Меню → содержит несколько основных операций с презентациями:
Присоединяет другое поле данных как презентацию к текущим данным. Следует отметить, что эта полезная функция иногда может вводить в заблуждение если пытаться получить нечто, основанное на данных, поскольку все расчётные значения получаются из нижележащих данных (а не из презентации, хоть она и выглядит как данные).
Удаляет презентацию из текущего окна данных. Этот вариант является альтернативой контекстного меню, доступного по щелчку правой кнопкой мыши в окне данных.
Извлекает презентацию из текущего окна данных в новое изображение того же файла. Таким способом можно извлечь данные презентации для дальнейшей обработки. Следует отметить, однако, что извлекаемые данные не содержат информации о реальном масштабе, поскольку презентация нужна для визуализации определённых особенностей, но получаемым данным трудно или невозможно присвоить физический смысл. Следовательно, диапазоном значений нового канала всегда будет [0, 1].
→ →
Простой и удобный способ увидеть данные как будто они освещаются с определённого направления. Направление может быть задано пользователем. Также возможно смешивать затенённое и исходное изображения для целей презентации. Разумеется, получающееся в результате изображение не имеет смысла с физической точки зрения.
→ →
Фильтры горизонтальных и вертикальных градиентов Собела и Превитта создают изображения, похожие на затемнение, однако, они выводят данные как результат свёртки данных с относительно стандартизованным ядром. Следовательно, они, например, могут использоваться для дальнейшей обработки презентаций. Ядра для горизонтальных фильтров приведены ниже, вертикальные ядра отличаются только отражением относительно главной диагонали.
→ →
Нередко возникает задача визуализации разрывов непрерывности, присутствующих на изображении, в частности, разрыв непрерывности значений (нулевого порядка) и непрерывности производных (первого порядка). Хотя методы обнаружения обоих называют методами «обнаружения края», они в реальности достаточно сильно отличаются, поэтому мы будем называть первые обнаружением ступеней и вторые как обнаружение края (кромки). Методы обнаружения более частных особенностей, т.е. углов, также широко используются, эти методы обычно относятся к нулевому порядку.
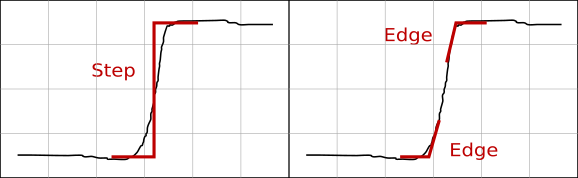
Порядок метода обнаружения разрывов непрерывности легко может быть виден на выводимом изображении. поскольку методы обнаружения краёв обычно дают типичные двойные линии на разрывах значений, как показано на следующем рисунке. В то время, как у идеальной ступеньки положения верхней и нижней кромки совпадают, данные реального мира имеют тенденцию содержать две отдельных кромки как показано на рисунке. Кроме того, нахождение двух кромок на ступеньке данных, даже на идеально острой, нередко является врождённой чертой методов обнаружения кромок.
В Gwyddion доступны следующие функции обнаружения ступеньки и кромки (последние являются в некоторой степени экспериментальными, с другой стороны обычно они дают лучшие результаты по сравнению с хорошо известными алгоритмами):
- Канни
Метод обнаружения края Канни – хорошо известный метод обнаружения ступеней и может быть использован чтобы извлекать изображения резких разрывов значений данных в виде тонких однопиксельных линий.
- Лапласиан гауссианов
Лапласиан представляет собой простую свёртку со следующим ядром (которая является пределом дискретного фильтра лапласиана гауссианов при σ → 0):
- Пересечение нуля
Алгоритм обнаружения края пересечением нуля помечает линии там, где результат фильтра лапласиана гауссианов меняет знак, т.е. пересекает ноль. Полуширина на половинной высоте гауссианов определяет уровень выделяемых деталей. Порог позволяет исключить смену знака со слишком малым абсолютным значением соседних пикселей, убирая мелкий шум. Следует заметить, однако, что для ненулевого порога линии краёв могут перестать быть непрерывными.
- Ступень
Алгоритм обнаружения ступеней обеспечивает хорошее разрешение, т.е. острые линии разрыва, и хороший динамический диапазон при этом будучи относительно нечувствителен к шуму. Принцип достаточно прост: он показывает квадратный корень разницы между квантилями 2/3 и 1/3 от значений данных в круговой окрестности радиусом в 2,5 пикселя с центром в каждом дискретном значении.
- Гауссова ступень
Гауссова ступень – настраиваемый фильтр, с балансом между точным отслеживанием ступеней и устойчивостью к шуму. Он имеет один настраиваемый параметр – ширину гауссовой функции (задаваемую как полная ширина на половине высоты). Узкие фильтры дают более тонкие линии, но также выделяют локальные дефекты. Широкие фильтры лучше отделяют ступени от других особенностей поверхности, но результат будет более размытым.
Фильтр работает путём расчёта свёртки изображения с ядрами, состоящими из гауссовой функции умноженной на функцию знака и повернутой чтобы покрывать различные направления. Результаты затем возводятся в квадрат и суммируются вместе.
- Ср. квадр.
Обнаружение ступеней показывает области с высоким локальным изменением значений. Рассчитывается и показывается среднеквадратичное отклонение от среднего значения в круговой окрестности радиуса 2,5 пикселя с центром в каждом дискретном значении.
- Кромка среднеквадратичного отклонения
Эта функция просто обрабатывает вывод среднеквадратичного отклонения фильтром, подобным лапласиану, чтобы усилить границы областей с большим локальным разбросом значений. Несмотря на имя это по прежнему средство обнаружения ступеней.
- Локальная нелинейность
Метод обнаружения края, который показывает локально сильно неплоские области. Он аппроксимирует плоскостью круговую окрестность радиусом в 2,5 пикселя с центром в каждом отсчёте и затем рассчитывает остаточную сумму квадратов аппроксимации, пересчитанную в наклон плоскости, т.е. делённую на 1 + bx2 + by2 где bx и by – коэффициенты плоскости в направлениях x и y, соответственно. Затем отображается квадратный корень величины.
- Наклон
Показывает угол ϑ наклона локальной плоскости. Технически эта функция относится к детекторам ступени, однако. выделение ступеней на результате вывода не слишком сильное и она больше предназначена для легкого визуального сравнения различных наклонов, представленных на изображении.

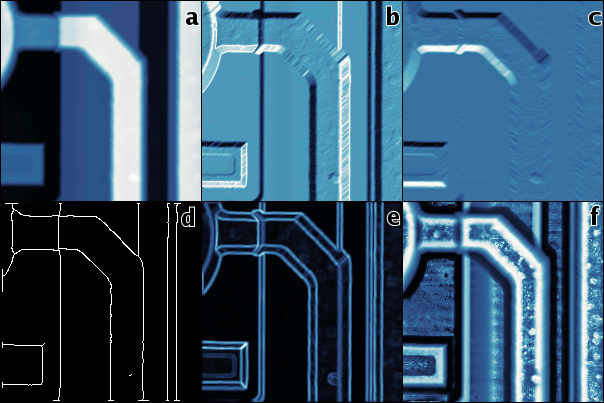
Сравнение методов обнаружения ступеней и кромок на нескольких интересных или типичных примерах данных. Канни и пересечение нуля – детекторы ступеней, которые выводят линии края шириной в один пиксель, ступень и наклон – детекторы ступеней с непрерывным выводом, локальная нелинейность – детектор кромки, детектирование кромки легко можно наблюдать на втором и третьем ряду. Следует отметить, что пересечение нуля можно настраивать, его параметры подбирались чтобы получить вменяемый результат для каждого примера.
→ →
Метод для показа деталей в областях, где присутствует большое и малое изменение значений одновременно. Это достигается расчётом диапазона локального изменения значений, или разброса, вокруг каждого отсчёта данных и растягивание его таким образом, чтобы сделать этот разброс одинаковым для всех данных.
→ →
Альтернативный метод улучшения локального контраста. Это выравнивающий фильтр верхних частот, чем-то противоположный медианному фильтру. Каждое значение пикселя преобразуется в его ранг среди всех значений в определённой окрестности. Радиус окрестности задаётся параметром размер ядра.
В результате получается что все локальные максимумы приводятся к одному одинаковому максимальному значению, все локальные минимумы к одинаковому минимальному и все значения, не являющиеся ни максимумом, ни минимумом преобразуются к диапазону между ними, основанному на их ранге. Поскольку результат применения фильтра с радиусом r может содержать максимально π(r + 1/2)2 различных значений (приблизительно), фильтр также приводит к дискретизации значений, особенно для малых размеров ядра фильтра.
→ →
Эта функция рисует на основе изображения топографии поверхности похожую на изображение РЭМ презентацию используя простейший возможный метод Монте-Карло. Для каждого пикселя поверхности выбирается некоторое количество отрезков, исходящих из этого пикселя со случайными направлениями и гауссовым распределением длин. Стандартное отклонение в распределении Гаусса управляется параметром радиус интегрирования. Если другой конец отрезка попадает в пустое пространство, яркость исходного пикселя увеличивается. Если он попадает внутрь материала, т.е. значение высоты оказывается ниже поверхности в конце отрезка, яркость уменьшается. Точнее, это описывает используемый метод Монте-Карло. Количеством отрезков можно управлять с помощью параметра качество. Эквивалентно, такое же значение интенсивности может быть рассчитано с помощью прямого интегрирования по всем пикселям в круговой окрестности заданной точки. Это соответствует методу Интегрирование.
Поскольку даже простой расчёт может требовать значительного времени, может оказаться полезным знать как его скорость зависит от выставленных параметров. Время расчёта для метода Интегрирование зависит только от радиуса интегрирования. Время расчёта для метода Монте-Карло, зависит в основном только от параметра Качество (также есть некоторая зависимость от локальной топографии поверхности).