Возможности обработки данных XYZ на данный момент достаточно ограничены. Большая часть анализа должна производиться после преобразования их в изображение — основной тип данных, для которого Gwyddion предлагает большой выбор функций их обработки.
Основные операции с данными XYZ в настоящий момент включают в себя объединение двух наборов точек, доступное в меню → . Объединение позволяет избежать создания точек с в точности совпадающими пространственными координатами. Вместо этого их значения усредняются – что включается опцией Усреднить совпавшие точки.
→
Gwyddion отлично работает с данными, снятыми на правильной сетке, т.е. данными изображения. Чтобы применить его функции обработки данных к нерегулярным данным XYZ, эти данные необходимо интерполировать на правильную сетку. Другими словами, данные нужно растеризовать.
Пользователю доступен выбор нескольких методов интерполяции, задаваемых опцией Тип интерполяции:
- Округление
Этот вариант интерполяции аналогичен интерполяции округлением для правильных сеток. Интерполированное значение в точке на плоскости равно значению ближайшей точки в наборе точек XYZ. Это означает. что проводится триангуляция Вороного и каждая ячейка Вороного «заполняется» значением ближайшей точки.
- Линейная
Этот вид интерполяции аналогичен линейной интерполяции для правильных сеток. Интерполированное значение в точке рассчитывается из значений трёх вершин треугольника триангуляции Делоне, содержащего точку. Поскольку три вершины определяют плоскость в пространстве уникальным образом, значение в точке определяется этой плоскостью.
- Поле
Значение в точке будет взвешенным средним всего набора точек XYZ, где вес обратно пропорционален четвёртой степени расстояния. Поскольку для каждой интерполированной точки рассматриваются все точки данных XYZ, этот метод может оказаться очень медленным.
- Среднее
Метод получения значений пикселей на лету используя комбинацию простого округления и переноса соседних значений. В плотных местах, где большое количество точек XYZ попадает в каждый пиксель, значение, присваиваемое пикселю будет некоторым вариантом взвешенного среднего точек. В местах с редким расположением точек, где относительно большие области не содержат точек XYZ, значение пикселя переносится с соседних пикселей, которые содержат точки XYZ. Основной особенностью данного метода интерполяции является то, что он всегда будет быстрым, в то же время нередко получается весьма неплохой результат интерполяции.
Первые два типа интерполяции основаны на тесселяции Вороного и триангуляции Делоне, которые плохо определены для наборов точек, где более двух точек лежит на одной линии и более трёх лежит на окружности. если это происходит, триангуляция может дать сбой и будет показано сообщение об ошибке.
Значения вне выпуклой оболочки множества точек XYZ на плоскости описываются опцией Тип внешней части:
- Граничный
Набор точек не меняется никоим образом и значения на выпуклой оболочке просто расширяются на бесконечность.
- Зеркальный
Набор точек дополняется точками, «отраженными» относительно сторон ограничивающего параллелепипеда.
- Периодический
Набор точек дополняется периодически повторяющимися точками из окрестности противоположной стороны ограничивающего параллелепипеда.
Горизонтальные и вертикальные размеры в пикселях для результирующего изображения задаются как Горизонтальный размер и Вертикальный размер в разделе Разрешение.
Нередко результирующее изображение должно иметь квадратные пиксели. Это может быть достигнуто нажатием кнопки . Данная функция не пытается сделать пиксели квадратными в процессе редактирования разрешения и диапазонов размеров чтобы не менять значения, которые вы хотели бы сохранить. Поэтому перевод в квадратные пиксели надо включить в явном виде этой кнопкой.
Возможно растеризовать только часть данных XYZ и также построить часть их окружения. Область для растеризации изображения управляется диапазонами, задаваемыми в разделе Физические размеры диалогового окна. Кнопка устанавливает область в прямоугольник, целиком содержащий данные XYZ. Также можно выбрать область для построения на изображении предпросмотра, естественно предполагая, что она лежит внутри показываемой сейчас на экране области.
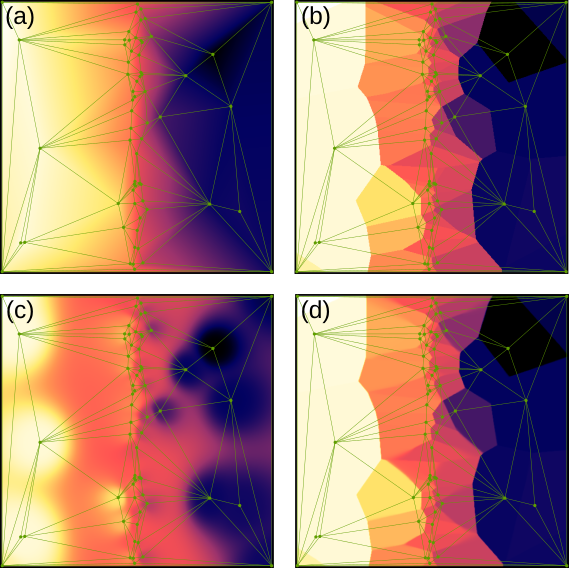
Триангуляция Делоне показанная в режиме (a) линейной интерполяции, (b) интерполяции округлением, (c) интерполяцией по всему полю и усреднением (d) для неправильного набора точек. Поскольку точки расположены достаточно редко, усреднение похоже на округление, только чуть размытое.
Если данные XYZ представляют собой изображение, т.е. точки формируют регулярную сетку, ориентированную вдоль осей декартовой системы координат, и каждая точка в прямоугольной области представлена только один раз, функция растеризации может сразу построить соответствующее изображение. Это можно сделать используя кнопку которая появляется вверху диалогового окна в данном случае.
→
→
Основная функция является той же самой, что и Исправить нуль для данных изображения. Она смещает все значения таким образом, чтобы их минимум стал равен нулю.
удаляет среднюю плоскость изображения. Эта функция предлагает два подхода. Вычитание полностью эквивалентно вычитанию плоскостидля изображений и представляет собой простое вычитание средней плоскости, которая определяется с помощью обычного метода наименьших квадратов.
Поворот удаляет среднюю плоскость реальным вращением облака точек, операцией которая может быть точно реализована только для данных XYZ (соответствующая функция Выровнять поворотом для изображений является приближенной). Более того, функция гарантирует что средняя плоскость будет горизонтальной после поворота, что соответствует удалению средней плоскости методом наименьших квадратов расстояний до этой плоскости (в отличие от вертикальных расстояний для изображений). Естественно, поскольку поворот смешивает пространственные координаты и значения данных, он будет возможен только если z является той же самой физической величиной, что и x, и y (предполагается, что геометрическими размерами).
Вращение меняет координаты x и y точек, потенциально делая данные XYZ несовместимыми с другими данными в файле. Включая Обновить X и Y всех совместимых данных можно обновить пространственные координаты во всех остальных наборах данных XYZ в файле, чтобы они соответствовали пространственным координатам в текущем после поворота. Значения z во всех остальных данных естественно остаются неизменными.
→
Эта функция также доступна для изображений. Описание различий между вариантами функции для изображений и данных XYZ можно найти в разделе Аппроксимировать форму для изображений.
Аппроксимация методом наименьших квадратов геометрическими фигурами и другими предопределёнными функциями всего набора данных может использоваться различными способами: для удаления общей формы, такой как сферическая, измерения геометрических параметров или создания идеализированных данных, соответствующих несовершенной реальной топографии. Также возможно использовать данный модуль для генерации искусственных данных если ничего не аппроксимировать и задать все геометрические параметры явным образом, хотя это всё равно требует обеспечить входные данные, которые будут задавать координаты XY точек.
Простейший вариант использования требует выбрать тип формы для аппроксимации, задаваемый как Тип функции, и нажать следующие три кнопки в заданном порядке:
Автоматическая начальная оценка параметров. Обычно первоначальной оценки достаточно чтобы перейти к аппроксимации. Если она слишком отличается от правильной может понадобиться подстроить некоторые из параметров вручную чтобы помочь аппроксимации методом наименьших квадратов найти правильный минимум. Для некоторых функций оценка использует случайную выборку из входных данных чтобы не занимать слишком много времени. Вследствие этого она является невоспроизводимой и нажатие этой кнопки снова может привести к несколько другой начальной оценке параметров.
Аппроксимация методом наименьших квадратов используя случайную выборку входных данных. Для большого набора входных данных работает гораздо быстрее, чем полная аппроксимация, при этом в большинстве случаев она сходится к набору параметров, достаточно близких к конечным. Позволяет быстро проверить будет ли метод наименьших квадратов сходиться к ожидаемому минимуму — и одновременно получить начальный набор параметров ближе к минимуму для последующей полной аппроксимации.
Полная аппроксимация методом наименьших квадратов используя полный набор данных. Может занять некоторое время, особенно для больших наборов входных данных и медленно вычисляемых функций.
Остаточная разница на одну точку в методе наименьших квадратов показана под вкладками как Среднеквадратичная разница. Она рассчитывается заново при каждом перерасчёте предпросмотра, т.е. не только после аппроксимации, но и после оценки и после подстройки параметров вручную.
Основные элементы управления на первой вкладке также позволяют выбрать, что будет выводиться в результате аппроксимации: либо аппроксимированная форма, либо разница между исходными данными и ней, либо оба.
Изображение предпросмотра может показывать либо входные данные, либо аппроксимирующую форму, либо разницу между ними двумя — что обычно оказывается наиболее полезным вариантом. Разница может быть показана с адаптированной шкалой цвета, где красный обозначает входные данные выше аппроксимирующей формы, синие ниже аппроксимации. Этот режим включается опцией Показывать различия с адаптированной шкалой цвета.
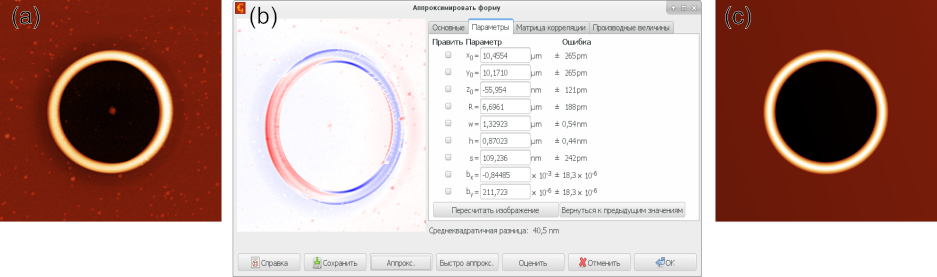
Пример аппроксимации формы: a) оригинальные данные топографии с кольцевой структурой на поверхности тонкой плёнки, b) диалоговое окно аппроксимации с параметрами справа и разницей между данными и аппроксимацией, показанной в левой части окна, c) результирующая аппроксимирующая форма.
Вкладка Параметры показывает значения всех параметров аппроксимации и их ошибок и позволяет осуществлять точный контроль за ними. Каждый параметр может быть свободным или зафиксированным. Зафиксированные параметры не меняются никакими аппроксимирующими и оценивающими функциями, они сохраняют то значение, которое вы ввели. Когда вы меняете значение параметра вручную, изображение предпросмотра не перерасчитывается заново — необходимо нажать чтобы обновить его. Кнопка позволяет вернуться к предыдущему набору параметров. Для оценки, аппроксимации или изменения вручную это означает набор значений параметров до того, как выполняемая операция их изменила. Для возврата к предыдущим это означает набор параметров до возврата — поэтому повторные нажатия на эту кнопку будут менять параметры между двумя последними наборами.
Вкладка Матрица корреляции показывает после успешной аппроксимации матрицу корреляции параметров. Коэффициенты корреляции, которые очень близки к единице (по модулю) будут подсвечены.
И наконец, вкладка Производные величины показывает различные полезные значения, рассчитанные из параметров аппроксимации. Некоторые функции не содержат производных величин, некоторые имеют несколько таких. Большая часть производных величин представляет собой параметры, которые могут оказаться более интересны для вас, чем действительные параметры аппроксимации, но плохо подходят для аппроксимации вследствие проблем с устойчивостью численного решения. Производные величины показываются с оценкой ошибок, рассчитанной используя законы распространения ошибок (включая корреляции параметров).
Типичным примером является кривизна сферической поверхности против её радиуса кривизны. В то время, как радиус является более привычным, он меняется от бесконечности до минус бесконечности когда поверхность меняется между выпуклой и вогнутой (т.е. когда становится очень близкой к плоской), что делает его неподходящим в качестве параметра аппроксимации. Кривизна, напротив, является нулевой для плоской поверхности. Следовательно, кривизна используется как параметр аппроксимации и радиус кривизны показывается как производная величина.