Les artefacts de convolution de sonde sont l'une des plus importantes sources d'erreurs des mesures SPM. Comme la sonde n'est jamais idéale (comme la fonction delta) on observe souvent un certain niveau de distorsion généré par cet effet. On peut même observer la sonde imagée sur l'image du scan alors que des détails fins sont présents sur la surface.
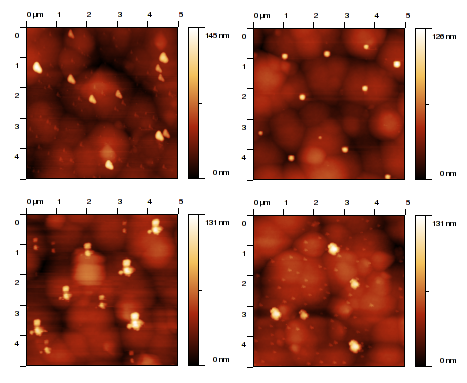
Images d'une surface de ZnSe mesurée avec quatre sondes différentes (plus ou moins en mauvais état).
Heureusement, on peut simuler et/ou corriger les effets des sondes à l'aide d'algorithme respectivement de dilatation et/ou d'érosion. Ces algorithmes ont été publiés par Villarubia (voir [1]).
Pour étudier l'influence de la sonde sur les données nous devons d'abord connaître sa géométrie. En général, celle-ci peut être déterminée de différentes façons :
- utiliser les données du fabricant (géométrie de lal sonde, rayon et angle de la pointe et tip geometry)
- utiliser un microscope électronique à balayage ou une technique similaire permettant de déterminer les propriétés de la sonde.
- utiliser un échantillon de caractérisation de sonde (ayant des bords raides).
- utiliser un algorithme d'estimation à l'aveugle en combinaison avec des échantillons de caractérisation de sonde ou d'autres échantillons adaptés.
Avec Gwyddion, nous pouvons utiliser la première et la dernière approche mentionnées. La plupart des géométries basiques des sondes peuvent être simulées à l'aide de la modélisation de sonde ( → → ). Cette manière de spécifier la géométrie peut être très efficace lorsque l'on souhaite simplement vérifier une carte d'incertitude ou effectuer une simulation de convolution de sonde.
Vous pouvez utiliser l'algorithme d'estimation à l'aveugle pour obtenir une structure de sonde plus détaillée (et plus réaliste) ( → → ).
L'algorithme d'estimation à l'aveugle dérive du fait que l'on peut directement voir certains détails de la sonde sur des points des données. L'algorithme itère sur toute la surface, et tente en chaque point de déterminer chaque point de la sonde en fonction de la pente la plus forte dans la direction allant du point de la sonde à sa pointe.
Gwyddion permet d'utiliser cet algorithm de deux manières : l'estimation partielle qui utilise un nombre de points limité parmi les plus élevés dans l'image, et l'estimation complète qui utiliser l'image entière (et qui ainsi bien plus lente). Le module d'estimation permet aussi d'utiliser l'estimation partielle comme point de départ de l'estimation complète. Ceci doit permettre d'améliorer la vitesse de calcul de l'estimation complète.
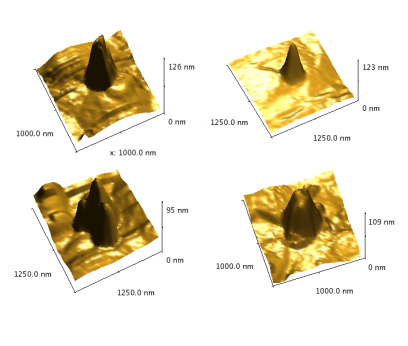
Sondes SPM obtenues à partir des données de la figure précédente en utilisant l'algorithme d'estimation à l'aveugle.
Lorsqu'on connaît la géométrie de la sonde, on peut utiliser l'algorithme de convolution (dilatation) de sonde afin de simuler le processus d'aquisition des données. Il faut dans ce cas utiliser le module Dilatation ( → → ). Ceci peut être utile lorsqu'on travaille sur des données résultant de simulations numériques (voir par exemple [2]).
Notez que ces algorithmes (ainsi que les deux qui suivent) nécessitent que les données du scan et de la sonde soient compatibles, c'est-à-dire que les dimensions physiques des pixels du scan et de l'image de la sonde soient identiques. Cette relation est naturellement obtenue par estimation à l'aveugle utilisée sur les mêmes données (ou des données correspondant à une mesure identique). Vous devrez ré-échantillonner l'image de la sonde si vous l'avez obtenue par un autre moyen.
L'opposé de la convolution de sonde correspond à la reconstruction de surface (érosion), que l'on peut utiliser pour corriger partiellement l'influence de la sonde sur les données. La fonction Reconstruction de Surface permet de réaliser cette opération ( → → ). Evidemment, les données correspondant à des points de l'image n'ayant pas été en contact avec la sonde (des pores par exemple) ne peuvent être reconstruites car il n'existe aucune information sur ces points.
Comme on peut le voir, les parties d'une images de scan posant le plus de problèmes sont les points où la sonde ne touche pas la surface en un seul point mais en plusieurs. On a une perte d'information pour ces points. L'algorithme de la carte d'incertitude permet de marquer les points pour lesquels la surface a été probablement touchée en un seul point.
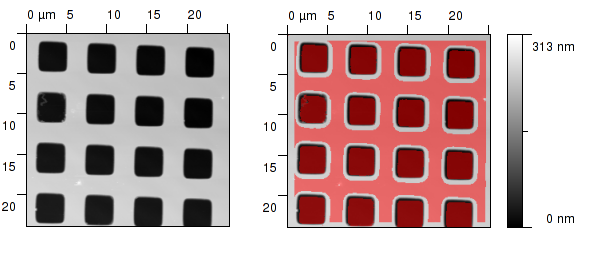
Cartes d'incertitude obtenue avec un réseau standard. Notez que les paramètres de la sonde modélisée ont été pris dans les données du fabricant pour des raisons d'illustration. A gauche : échantillon, à droite : échantillon avec la carte d'incertitude.
L'algorithme de la carte d'incertitude permet donc de marquer sur l'image les données corrompues de manière définitice par la convolution de la sonde. Il est important de vérifier la présence de ces points lors de l'analyse de données de surfaces présentant de fortes pentes. Vous pouvez utiliser la fonction Carte d'Incertitude de Gwyddion pour créer ces cartes ( → → ).
[1] J. S. Villarubia, J. Res. Natl. Inst. Stand. Technol. 102 (1997) 425.
[2] P. Klapetek, I. Ohlídal, Ultramicroscopy, 94 (19-29), 2003