Les possibilités de traitement des données XYZ sont actuellement plutôt limitées. L'analyse doit être faite après conversion en image – le type de données basique pour lequel Gwyddion propose de nombreuses fonctions.
→
Gwyddion est un logiciel particulièrement puissant pour traiter des données échantillonnées selon une grille régulirère, c'est-à-dire une image pixellisée. Pour appliquer des fonctions de traitement à des données XYZ irrégulières, les données doivent d'abord être interpolées selon une grille régulière, c'est-à-dire rastérisée.
Plusieurs méthodes d'interpolations sont proposées, elles peuvent être choisies à l'aide de l'option type d'interpolation type :
- Arrondi
Cette interpolation est analogue à l'interpolation arrondie pour les grilles régulières. La valeur interpolée en un point du plan est égale à la valeur du point le plus proche dans l'ensemble des points XYZ. Cela signifie que le pavage de Voronoi est utilisé et que chaque cellule de Voronoi est « remplie » avec la valeur du point le plus proche.
- Linéaire
Cette interpolation est analogue à l'interpolation linéaire pour les grilles régulières. La valeur interpolée en un point est calculée à partir des trois vertex du triangle contenant le point obtenu par triangulation de Delaunay. Comme les troix vertex déterminent un plan unique de l'espace, la valeur en ce point est définie par ce plan.
- Global
La valeur en un point correspond à la moyenne pondérée de tous les points XYZ de l'ensemble des données, où le poids est proportionnel à l'inverse de la puissance quatrième de la distance mutuelle. Cette méthode peut être très lente car toutes les coordonnées XYZ sont utilisées pour le calcul de chaque point.
- Moyenne
Méthode ad hoc déterminant la valeur des pixels en combinant le moyennage et la propagation. Dans les zones denses où plusieurs points XYZ tombent dans le même pixel la valeur attribuée est approximativement une moyenne pondérée des valeurs des points. Dans les zones pauvres dans lesquelles de larges espaces ne contiennes aucun point XYZ la valeur du pixel est propagée à partir des pixels les plus proches contenant quelques points XYZ. Le principal intérêt de ce type d'interpolation est qu'il est toujours rapide tout en produisant un résultat acceptable.
Ces deux derniers types d'interpolation sont basés sur la triangulation de Delaunay et le pavage de Voronoi, celles-ci étant mal définie pour les ensembles de points contenant plus de deux points disposés sur une même ligne ou plus de trois points placés sur un cercle. Dans ces cas précis, la triangulation échoue et le module d'import affiche une message d'erreur.
Les valeurs en dehors de l'ensemble des points XYZ sont influencées par le Type d'exterieur:
- Bord
L'ensemble des points n'est pas modifié et les valeurs présentes sur le bord de l'ensemble des points sont étendues à l'infini.
- Miroir
Des points « réfléchis » par rapport aux côtés du volume limite sont ajoutés à l'ensemble des points.
- Periodique
Des points répétés périodiquement par rapport aux côtés opppsés du volume limite sont ajoutés à l'ensemble des points.
Les dimensions horizontale et verticale des pixels de l'image résultante sont spécifiés par les paramètres taille horizontale et taille verticale dans la section résolution.
En général, l'image résultante devra avoir des pixels carrés. Cette condition peut être réalisée en pressant le bouton . La fonction n'essaie pas de forcer les pixels carrés lors de la modification de la résolution et des plages de données pour éviter de modifier des valeurs que vous souhaiteriez conserver. Vous devrez donc à un moment ou un autre forcer explicitement les pixels carrés avec ce bouton.
Il est possible de ne rastériser qu'une portion des données XYZ ainsi que faire le rendu d'une partie de l'extérieur. La région à convertir en image est contrôlée par les plages spécifiées dans la section dimensions physiques. Le bouton ajuste la région à un rectangle contenant toutes les données XYZ. Il est aussi possible de sélectionner la région à rastériser sur l'aperçu, à condition qu'elle reste confinée dans la région en cours d'affichage.
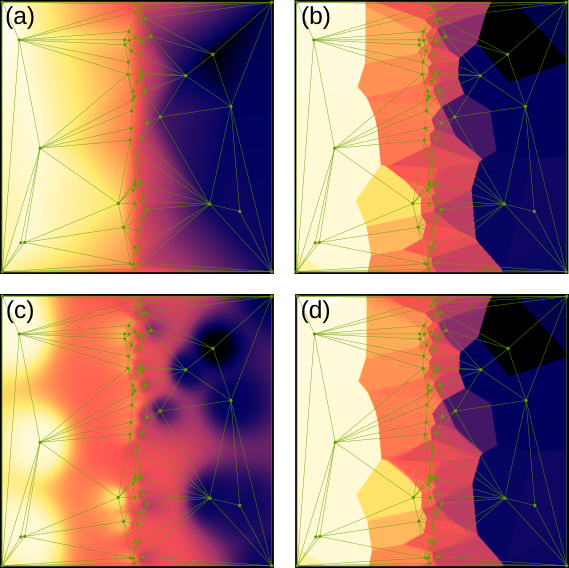
Triangulation de Delaunay affichée avec l'interpolation (a) linéaire, (b) arrondie, (c) globale et (d) moyenne d'un ensemble de points irrégulièrement espacés. Comme les points sont relativement espacés, l'interpolation moyenne est assez similaire à l'arrondie, avec seulement quelques zones adoucies en plus.
Si les données XYZ représentent une image, c'est-à-dire que les points forment une grille régulière le long des axes cartésiens avec des points uniques sur la grille rectangulaire, alors la fonction de rastérisation peut directement produire l'image correspondante. Cette action peut être réalisée en utilisant le bouton qui apparaît dans ce cas en haut de la fenêtre de dialogue.
→
→
La fonction est exactement la même que fizer le zéro des données images. Elle décale toutes les valeurs de manière à ce que le minimum valle zéro.
La fonction supprime le plan moyen. Celle-ci propose deux méthodes. La soustraction est complètement analogue à la fonction niveau plan pour les données images et consiste en une simple soustraction du plan moyen déterminée par la méthode des moindres carrés.
La rotation supprime le plan moyen à l'aide d'une véritable rotation du nuage de points, une opération uniquement réalisable de manière exacte sur des données XYZ (la fonction rotation de plan pour les images est approximée). De plus, la fonction garantit un niveau moyen horizontal après rotation, ce qui correspond à la suppression du plan moyen au sens rigoureux des moindres carrés. Bien évidemment, étant donnée que la rotation mélanges les coordonnées latérales et les valeurs des données, celle-ci n'est possible que lorsque z est de même quantité physique que x et y (en général une longueur).
La rotation change les coordonnées x et y des points, rendant potentiellement les données XYZ incompatibles avec les autres données du fichier. En activant la case mettre à jour les valeurs X et Y de toutes les données compatibles vous pouvez mettre à jour les coordonnées latérales de tous les autres ensembles de points XYZ du fichier de manière à ce qu'elles correspondent à celle de l'ensemble courant après rotation. Les valeurs z des autres données sont bien entendu conservées.
→
Cette fonction est aussi disponible pour les images. Voir le chapitre l'ajustement de forme des images concernant les différences entre les données images et XYZ.
L'ajustement par la méthode des moindres carrés de formes géométriques ou d'autres fonctions prédéfinies sur les données peut servir différents besoins : suppression d'une forme globale telle qu'une surface sphérique, mesure de paramètres géométriques ou création de données idéales correspondant à une topographie réelle imparfaite. Il est aussi possible d'utiliser le module pour générer des données artificielles dans le cas où rien n'est ajusté et que les paramètres géométriques sont entrés explicitement, bien qu'il soit nécessaire de fournir en entrée les données définissant les points XY.
L'utilisation de base consiste d'abord à choisir le type de forme, à sélectionner dans la liste type de fonction, puis à presser les trois boutons suivants dans l'ordre :
Estimation initiale automatique des paramètres. En général l'estimation initial est suffisante pour procéder à l'ajustement. Lorsqu'elle est trop éloignée il peut être nécessaire d'ajuster certains paramètres manuellement pour aider l'agorithme à trouver le bon minimum. Pour certaines fonctions l'estimation utilise un sous-ensemble des données choisi aléatoirement pour éviter un temps de calcul trop long. L'estimation est donc non déterministe et le fait de presser à nouveau le bouton peut aboutir à une estimation sensiblement différente des paramètres.
Ajustement par la méthode des moindres carrés utilisant un sous-ensemble des données choisi aléatoirement. Le calcul est nettement plus rapide que l'ajustement complet dans le cas de données de taille importante, et dans la plupart des cas il convergera vers des paramètres proches des valeurs finales. Il permet de rapidement vérifier si la méthode des moindres carrés va converger vers le minimum attendu – et obtenir au passage des valeurs de paramètres assez proches de ce minimum pour l'ajustement final.
Ajustement complet utilisant toutes les données. Cette opération peut prendre un certain temps, en particulier pour des données de taille importante ainsi que pour des fonctions prenant du temps à calculer.
La moyenne quadratique des écarts de chaque point est affichée sous les onglets, indiquée par différence quadratique moyenne. Celle-ci est recalculée lorsque l'aperçu est modifié, c'est-à-dire non seulement après un ajustement mais aussi après une estimation ou une modification manuelle.
Les contrôles de base du premier onglet permet aussi de sélectionner la sortie de l'ajustement, qui peut être la forme ajustée, la différence entre les données d'entrée et la forme ajustée, ou bien les deux.
L'aperçu peut afficher les données d'entrée, la forme ajustée ou bien la différence des deux – ce qui est généralement l'option la plus utile. La différence peut être affichée avec une échelle de couleur adaptée pour laquelle du rouge signifie que les données d'entrée sont au-dessus de la forme ajustée, et du bleu que les données d'entrée sous en-dessous de la forme ajustée. Cette échelle de couleur est utilisée en activant la case afficher l'écart avec une échelle de couleur adaptée.
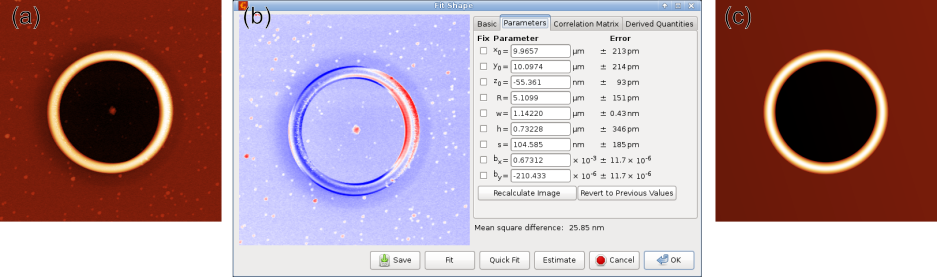
Exemple d'ajustement de forme : (a) données topographiques initiale d'une structure en anneau à la surface d'une couche mince, (b) fenêtre d'ajustement avec les paramètres du côté droit et la différence entre les données et l'ajustement dans la partie gauche, (c) forme ajustée résultante.
L'onglet paramètres affiche les valeurs de tous les paramètres d'ajustement ainsi que leur incertitude, et permet aussi leur contrôle précis. Chaque paramètre peut être fixé ou variable. Les paramètres fixés ne sont pas modifiés lors d'une estimation ou d'un ajustement ; ils conservent la valeur que vous avez entrée. Lorsque vous changez manuellement la valeur d'un paramètre, l'aperçu n'est pas mis à jour automatiquement – pour ce faire pressez le bouton . Le bouton permet d'afficher l'ensemble des valeurs précédentes. Lors d'une estimation, d'un ajustement ou d'une modification manuelle cela signifie que l'ensemble des valeurs des paramètres avant l'opération les modifiant sera restauré. Un nouvel appui fera revenir l'ensemble des valeurs obtenu après l'opération – ce qui veut dire que l'appui répété sur le bouton fera alterner les deux derniers ensembles de valeurs.
L'onglet matrice de corrélation affiche, après un ajustement réussi, la matrice de corrélation. Les coefficients de corrélation très proches de un (en valeur absolue) sont mis en évidence.
Et pour finir, l'onglet quantités dérivées affiche diverses valeurs utiles obtenues à partir des paramètres d"ajustement. Certaines fonctions d'ajustement ne proposent aucune quantité dérivéee, d'autres en donnent plusieurs. La plupart des quantités drivées correspondent à des paramètres que vous pourriez trouver plus intéressantes que les paramètres d'ajustement eux-mêmes, mais qui s'avèrent incompatibles avec l'ajustement pour des raisons de stabilité numérique. Les quantités dérivées sont affichées accompagnées de leur incertitude, déterminées à l'aide de la loi de propagation des erreurs (incluant les corrélations entre paramètres).
L'exemple typique est la courbure d'une surface sphérique comparée à son rayon de courbure. Le rayon de courbure est plus communément utilisé mais il passe de plus l'infini à moins l'infini lorsque la surface passe de convexe à concave (c'est-à-dire lorsque la surface est pratiquement plane), ce qui le rend inutilisable comme paramètre d'ajustement. A contrario, la courbure d'une surface plane est nulle. C'est pour cette raison que la courbure est utilisée en paramètre d'ajustement, et que le rayon de courbure est affiché dans les quantités dérivées.