Many three-dimensional geometrical shapes that can be fitted by the image and XYZ Fit Shape functions have common parameters. Therefore, we first describe the shared parameters and only list the specific parameters in the descriptions of individual fitable geometrical shapes.
- x0
Horizontal position of the feature centre, usually coinciding with the apex (or the deepest point for negative-height features). For periodic shapes it is offset of one of the infinitely many features from the coordinate origin.
- y0
Vertical position of the feature centre, usually coinciding with the apex (or the deepest point for negative-height features). For periodic shapes it is offset of one of the infinitely many features from the coordinate origin.
- z0
Height of the base plane (at the feature centre if the base plane is inclined). Note that this parameter may be 100% correlated with other height-related parameters if a feature covers the entire image and the base plane is not visible.
- h
Height of the feature with respect to the flat base plane.
- φ
Rotation in the positive direction with respect to the basic orientation, which is usually with major axes of the shape aligned horizontally and vertically.
- bx
Slope of the base plane in the horizontal direction.
- by
Slope of the base plane in the vertical direction.
- a
Anisotropy parameter. It is equal to the ratio of the longer and shorter sides (or half-axes or other measures of width) of the feature. Therefore, the one dimension is equal to the mean dimension multiplied by √a and the other to the mean dimension divided by √a. Fix a to unity if the shape should not be elongated in one direction and contracted in another.
Bump-type shapes include base plane parameters bx and by and generally some parameter desribing the size of the shape at the base. If only the apex is present in the image, their values are undefined or they cease to be independent. This may cause the fit to converge poorly or fail. The parameter values need to be fixed in such case.
The Gaussian-smoothed bumps – cone and pyramids – have the following two common parameters:
- R
Radius of curvature at the apex.
- α
Tangent of the slope of the side.
- h
Height of the step above the base plane.
- δ
Smoothness, defining the width of error function-shaped edge between lower and upper planes.
- L
Period, i.e. the distance after which the structure starts repeating.
- p
Coverage, i.e. the portion of the plane where there is some feature, as opposed to the base plane.
Grating (simple) has only a single additional parameter controlling the shape, c. The ridge has the form of truncated hyperbolic cosine, with small c corresponding to a parabolic cross-section while large c corresponding to sharp, almost rectangular cross-section.
Grating (3-level) has a cross-section of three trapezoids stacked on top of another. The corresponding three height parameters h1, h2 and h3 determine the heights of the individual trapezoids. The corresponding width reduction parameters q1, q2 and q3 determine how much the upper base of the corresponding trapezoid is reduced with respect to the lower base (by the factor 1/(1 + qi)). It is often useful to look at the corresponding derived quantities L0, L1, L2 and L3 that are directly equal to the widths and derived quantity h equal to the total height.
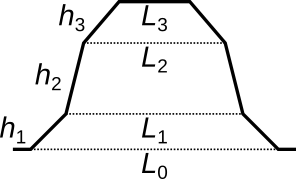
Widths and heights of the trapezoids forming the 3-level grating profile. Note that the widths are derived quantities, not direct fitting parameters.
Holes have parameters s which controls the tapering of the hole due to sloped sides and r which controls the radius of the rounder corners. For both parameters zeros correspond to an ideal rectangular shape.
Parabolic ring is a three-dimensional rotationally symmetric version of the Parabolic step fitting function and has exactly the same shape parameters.
Sphere has only one shape parameter C defining its curvature. The radius is available as a derived quantity.
Cylinder (lying) also has a curvature parameter C. In addition it has a inclination parameter b∥ determining the base plane inclination along the cylinder length.
Gaussian width is controlled by the mean rms parameter σmean. For anisotropic Gaussians it is equal to the geometric mean of the two widths in the orthogonal directions that are available as derived quantities.
Lorentzian mean half width at half maximum is βmean. For anisotropic Lorentzian it is equal to the geometric mean of the two widths in the orthogonal directions that are available as derived quantities.
Cone parameter R determines the cone radius at base.
Pyramid (diamond) and Pyramid (3-sided) parameter L determines the pyramid side at base. Since the basic orientation of this pyramid is diagonal all four sides still have the same length even when the anisotropy parameter a is not unity.
Step (two-sided) has parameter w defining the step width.